基于python实现CNN卷积层及卷积运算优化学习

推导过程：

符号说明：

DNN反向传播原理

卷积层反向传播推导

前向传播：

im2col的实现

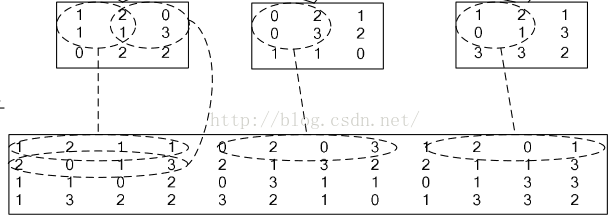
im2col()：输入数据根据滤波器、步幅等展开的二维数组，每一行代表一条卷积输入数据

卷积就是卷积核跟图像矩阵的运算。卷积核是一个小窗口，记录的是权重。卷积核在输入图像上按步长滑动，每次操作卷积核对应区域的输入图像，将卷积核中的权值和对应的输入图像的值相乘再相加，赋给卷积核中心所对应的输出特征图的一个值。

im2col的作用就是优化卷积运算，如何优化呢，我们先学习一下这个函数的原理。
我们假设卷积核的尺寸为2×2，输入图像尺寸为3×3.im2col$做的事情就是对于卷积核每一次要处理的小窗，将其展开到新矩阵的一行（列），新矩阵的列（行）数，就是对于一副输入图像，卷积运算的次数（卷积核滑动的次数）

---

以最右侧一列为例，卷积核为2*2，所以新矩阵的列数就为4；步长为一，卷积核共滑动4次，行数就为4.

看到这里我就产生了一个疑问：我们把一个卷积核对应的值展开，到底应该展开为行还是列呢？卷积核的滑动先行后列还是相反？区别在哪？
这其实主要取决于我们使用的框架访存的方式。计算机一次性读取相近的内存是最快的，尤其是当需要把数据送到GPU去计算的时候，这样可以节省访存的时间，以达到加速的目的。不同框架的访存机制不一样，所以会有行列相反这样的区别。在caffe框架下，im2col是将一个小窗的值展开为一行，而在matlab中则展开为列。所以说，行列的问题没有本质区别，目的都是为了在计算时读取连续的内存。
这也解释了我们为什么要通过这个变化来优化卷积。如果按照数学上的步骤做卷积读取内存是不连续的，这样就会增加时间成本。同时我们注意到做卷积对应元素相乘再相加的做法跟向量内积很相似，所以通过im2col将矩阵卷积转化为矩阵乘法来实现。

代码实现

python

import numpy as np
def im2col2(input_data, fh, fw, stride=1, pad=1):
    '''
     input_data--输入数据，shape为(batch_size,Channel,Height,Width)
     fh -- 滤波器的height 3
     fw --滤波器的width 3
     stride -- 步幅 1
     pad -- 填充 1
     Returns :
     col -- 输入数据根据滤波器、步幅等展开的二维数组，每一行代表一条卷积数据
    '''
    N, C, H, W = input_data.shape   "[20,1,28,28]"

    out_h = (H + 2 * pad - fh) // stride + 1    "[28]"
    out_w = (W + 2 * pad - fw) // stride + 1     "[28]"

    img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], "constant") 
     
    "[30*30*1]"
   

    col = np.zeros((N, out_h, out_w, fh * fw * C))  "fh * fw * C 负责存储每次参与卷积的参数"
    print(col.shape)
    # 将所有维度上需要卷积的值展开成一行（列）,卷积次数为out_h*out_w*c,每次卷积内含参数量为（fh*fw*c）
    for y in range(out_h):
        y_start = y * stride
        y_end = y_start + fh
        for x in range(out_w):
            x_start = x * stride
            x_end = x_start + fw
            col[:, y, x] = img[:, :, y_start:y_end, x_start:x_end].reshape(N, -1)

    col = col.reshape(N * out_h * out_w, -1)
    return col


def col2im2(col, out_shape, fh, fw, stride=1, pad=0):
    '''

     col: 二维数组
     out_shape-- 输出的shape，shape为(Number of example,Channel,Height,Width)
     fh -- 滤波器的height
     fw --滤波器的width
     stride -- 步幅
     pad -- 填充

     Returns :
     img -- 将col转换成的img ，shape为out_shape
    '''
    N, C, H, W = out_shape

    col_m, col_n = col.shape

    out_h = (H + 2 * pad - fh) // stride + 1

    out_w = (W + 2 * pad - fw) // stride + 1

    print("out_h,out_w",out_h,out_w)
    img = np.zeros((N, C, H, W))
    #img = np.pad(img,[(0,0),(0,0),(pad,pad),(pad,pad)],"constant")

    # 将col转换成一个filter
    for c in range(C):
        for y in range(out_h):
            for x in range(out_w):
                col_index = (c * out_h * out_w) + y * out_w + x
                ih = y * stride
                iw = x * stride
                img[:, c, ih:ih + fh, iw:iw + fw] = col[col_index].reshape((fh, fw))
    return img

测试：

输入input_data=[20,1,28,28]; fh=fw=3;采用SAME方式填充，则卷积的shape与input_data相同；

共卷积次数为15680次，每次卷积时input_data参与卷积的像素点数为9（卷积核为3*3）；所以col大小应为（15680，9）

程序输出结果：

python

"测试"
x=np.random.uniform(0,255,(20,1,28,28))
out = im2col2(x,3,3)
print(out.shape)  “(15680, 9)”

卷积层实现;

python

class Convolution:
    def __init__(self, W, fb, stride=1, pad=1):
        """
        W-- 滤波器权重，shape为(FN,NC,FH,FW),FN 为滤波器的个数
        fb -- 滤波器的偏置，shape 为(1,FN)
        stride -- 步长
        pad -- 填充个数
        """
        self.W = W
        self.fb = fb
        self.stride = stride
        self.pad = pad

        self.col_X = None
        self.X = None
        self.col_W = None

        self.dW = None
        self.db = None
        self.out_shape = None

    #    self.out = None

    def forward(self, input_X):
        """
        input_X-- shape为(m,nc,height,width)
        """
        self.X = input_X
        FN, NC, FH, FW = self.W.shape

        m, input_nc, input_h, input_w = self.X.shape


       # 将输入数据展开成二维数组，shape为（m*out_h*out_w,FH*FW*C)
        self.col_X = col_X = im2col2(self.X, FH, FW, self.stride, self.pad)
        print("self.col_X.shape",self.col_X .shape)
        # 将滤波器一个个按列展开(FH*FW*C,FN)       col_W.shape 15680,9 col_w 9,20  输出 15680，20
        self.col_W = col_W = self.W.reshape(FN, -1).T
        out = np.dot(col_X, col_W) + self.fb

        out = out.T #     20，15680

        out = out.reshape(m, FN, input_h, input_w)
        self.out_shape = out.shape
        print("out.shape", out.shape)
        return out #(20, 20, 28, 28)

    def backward(self, dz, learning_rate):
        print("==== Conv backbward ==== ")
        assert (dz.shape == self.out_shape)

        FN, NC, FH, FW = self.W.shape #[20,1,28,28]
        o_FN, o_NC, o_FH, o_FW = self.out_shape #[20,20,28,28]

        print("o_FN = {0}, o_NC = {1}, o_FH = {2}, o_FW = {3} ".format(o_FN,o_NC,o_FH,o_FW))

        col_dz = dz.reshape(o_NC, -1)  #col_dz  [20,15680]   dz[20, 20, 28, 28]

        col_dz = col_dz.T

        print("self.col_X.T,col_dz",self.col_X.shape,col_dz.shape)
        self.dW = np.dot(self.col_X.T, col_dz)  # [15680,9]  [15680,20]


        self.db = np.sum(col_dz, axis=0, keepdims=True)

        self.dW = self.dW.T.reshape(self.W.shape)
        self.db = self.db.reshape(self.fb.shape)
        print("dw.shape = {0},db.shape = {1} ,self.col_W={2}".format(self.dW.shape, self.db.shape,self.col_W.shape))
        d_col_x = np.dot(col_dz, self.col_W.T)  # shape is (m*out_h*out_w,FH,FW*C)
        print("d_col_x.shape= ", d_col_x.shape)
        dx = col2im2(d_col_x, self.X.shape, FH, FW, stride=1)
        print("dx.shape= ",dx.shape)
        assert (dx.shape == self.X.shape)

        # 更新W和b
        self.W = self.W - learning_rate * self.dW
        self.fb = self.fb - learning_rate * self.db

        return dx

测试：

python

'''
数据载入
'''
x=np.random.uniform(0,255,(20,1,28,28)) #测试集采用[20,1,28,28]
w=np.random.uniform(0,1,(20,1,3,3))   #卷积核采用通道数为1的3*3的卷积核，卷积次数为20
b=x=np.random.uniform(0,1,(1,20)) 
dz=np.random.uniform(0,255,(20,20,28,28))#dz.shape与前向传播大小相同

python

'''
正向与反向传播测试
'''



test = Convolution(w,b)
test.forward(x)
test.backward(dz,0.01)

forward()内部变量输出：

self.col_X.shape (15680, 9)

out.shape (20, 20, 28, 28)

与设计思想相符合

backward()内部变量输出输出值

dz.shape = (20, 20, 28, 28),col_dz.shape = (20, 15680)
dw.shape = (20, 1, 3, 3),db.shape = (1, 20)
d_col_x.shape= (15680, 9)
dx.shape= (20, 1, 28, 28)

代码源文件

基于python实现卷积层.py

tensflow实现卷积层

Code

import tensorflow as tf
import numpy as np

def conv2d_answer():
    with tf.Graph().as_default():
        
        # [N, height, width, channels] 4-D的tensors
        #占位符
        input_x = tf.placeholder(tf.float32, [30, 28, 28, 1], name='input_x') 
        
        x = np.ones(shape=[30, 28, 28, 1])

        #卷积核变量
        filter_w = tf.get_variable(
            'w', initializer=tf.truncated_normal(shape=[3, 3, 1, 20])
        )
        filter_b = tf.get_variable(
            'b', initializer=tf.zeros(20)
        )
        strides = [1, 2, 2, 1]  # 标准的写法。
        pad = 'VALID'
    
        conv_output = tf.nn.conv2d(
            input=input_x, filter=filter_w, strides=strides, padding=pad
        )
        print(conv_output.get_shape())
        conv_output = conv_output + filter_b
        # print(conv_output)
        # fixme 高级api
        conv_output1 = tf.layers.conv2d(
            inputs=input_x, kernel_size=7, filters=20, strides=2, padding='valid',
            use_bias=True
        )
        print(conv_output1.get_shape())
        # with tf.Session() as sess:
        #     sess.run(tf.global_variables_initializer())
        #     print(sess.run(conv_output, feed_dict={input_x: x}))

if __name__ == '__main__':
    conv2d_answer()

tensflow卷积层通过函数 tf.nn.conv2d 或者tf.layers.conv2d实现，

"""
    tf.nn.conv2d(input,    # 卷积的输入，必须是一个4-D tensor对象
        filter,            # 滤波器
        strides,           # 步幅
        padding,           # 填充方式  string:  'SAME'   or  'VALID'
        data_format="NHWC",   # 对输入数据格式的要求，[N, height, width, channels]； 也可以是另一种格式："NCHW"
        dilations=[1, 1, 1, 1], 
        name=None)
    """

caffe

在Caffe中是使用src/caffe/util/im2col.cu中的im2col和col2im来完成矩阵的变形和还原操作，即为上方python实现的代码，将卷积运算转化为矩阵相乘，提升了运算速度。

总结：

相比于现有框架，我的卷积运算部分还有待优化。实现了以矩阵相乘实现卷积运算，但是内存利用率低，可以用加速GEMM进行提高。

探究：如何优化卷积运算速度

提升卷积层运算速度，主要在于提高卷积的计算速度。

朴素卷积（Naive Convolution）

Code

'''Convolve `input` with `kernel` to generate `output`    
input.shape = [input_channels, input_height, input_width]    
kernel.shape = [num_filters, input_channels, kernel_height, kernel_width]    
output.shape = [num_filters, output_height, output_width]
'''
for filter in 0..num_filters    
    for channel in 0..input_channels        
        for out_h in 0..output_height            
            for out_w in 0..output_width                
                for k_h in 0..kernel_height    
                   for k_w in 0..kernel_width   
                    output[filter, channel, out_h, out_h] +=   
                    kernel[filter, channel, k_h, k_w] *    
                    input[channel, out_h + k_h, out_w + k_w]

涉及到了6个for嵌套循环，最内的循环进行了两次浮点运算（乘和加）。对于实验所使用的卷积层规模，它执行了8516万次，即该卷积需要1.7亿次浮点运算（170MFLOPs）。

内存访问同样需要时间：无法快速获取数据则无法快速处理数据。上述高度嵌套的for-loop使得数据访问非常艰难，从而无法充分利用缓存。

探究问题：如何访问正在处理的数据，以及这与数据存储方式有何关联。

逻辑上我们将矩阵/图像/张量看作是多维度的，但实际上它们存储在线性、一维的计算机内存中。我们必须定义一个惯例，来规定如何将多个维度展开到线性一维存储空间中，反之亦然。

大部分现代深度学习库使用行主序作为存储顺序。这意味着同一行的连续元素被存储在相邻位置。对于多维度而言，行主序通常意味着：在线性扫描内存时第一个维度的变化速度最慢。

从卷积到矩阵相乘

采用矩阵相乘替换朴素卷积

卷积是滤波器和输入图像块（patch）的点乘。如果我们将滤波器展开为2-D矩阵，将输入块展开为另一个2-D矩阵，则将两个矩阵相乘可以得到同样的数字。将图像块展开为矩阵的过程叫做im2col（image to column）。我们将图像重新排列为矩阵的列，每个列对应一个输入块，卷积滤波器就应用于这些输入块上。

在现实中，不同图像块之间通常会有重叠，因而im2col可能导致内存重叠。生成im2col 缓冲（im2col buffer）和过多内存（inflated memory）所花费的时间必须通过GEMM(矩阵乘优化)实现的加速来抵消。

加速GEMM

缓存

RAM是大的存储空间，但速度较慢。CPU缓存的速度要快得多，但其规模较小，因此恰当地使用CPU缓存至关重要。但是并不存在明确的指令：「将该数据加载到缓存」。该过程是由CPU自动管理的。

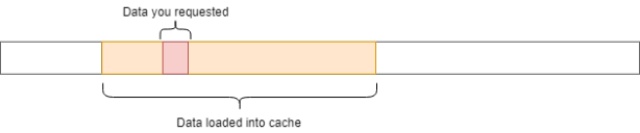
每一次从主内存中获取数据时，CPU会将该数据及其邻近的数据加载到缓存中，以便利用访问局部性（locality of reference）。

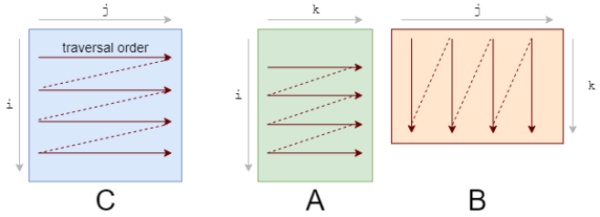
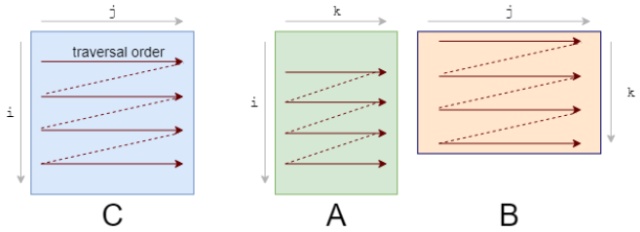
你应该首先注意到我们访问数据的模式。我们按照下图A的形式逐行遍历数据，按照下图B的形式逐列遍历数据。

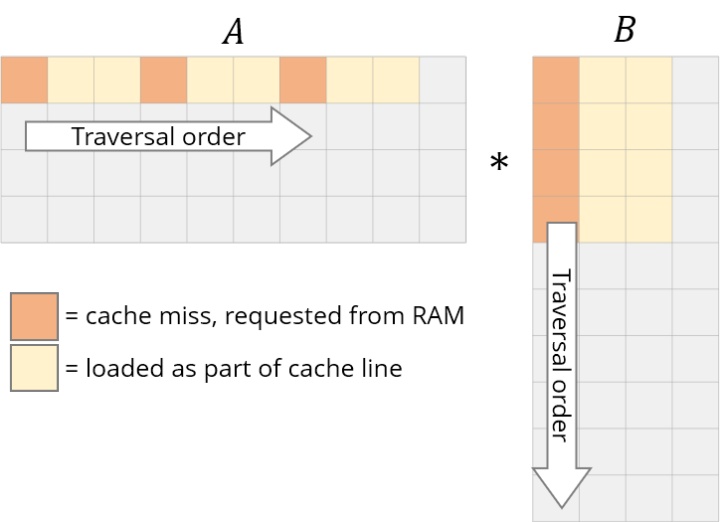
它们的存储也是行优先的，因此一旦我们找到 A[i, k]，则它在该行中的下一个元素A[i, k+1]已经被缓存了。接下来我们来看B中发生了什么：

• 列的下一个元素并未出现在缓存中，即出现了缓存缺失（cache miss）。这时尽管获取到了数据，CPU也出现了一次停顿。
• 获取数据后，缓存同时也被 B 中同一行的其他元素填满。我们实际上并不会使用到它们，因此它们很快就会被删除。多次迭代后，当我们需要那些元素时，我们将再次获取它们。我们在用实际上不需要的值污染缓存。

我们需要重新修改loop，以充分利用缓存能力。如果数据被读取，则我们要使用它。这就是我们所做的第一项改变：循环重排序（loop reordering）。

Code

for i in 0..M:    
    for j in 0..N:        
        for k in 0..K:            
            C[i, j] += A[i, k] * B[k, j]

将i,j,k 循环重新排序为 i,k,j：

Code

for i in 0..M:    
    for k in 0..K:        
        for j in 0..N:

乘/加的顺序对结果没有影响。而遍历顺序则变成了如下状态：

速度大大提升。

平铺（Tiling）

要想进一步改进重排序，我们需要考虑另一个缓存问题。

对于A中的每一行，我们针对B中所有列进行循环。而对于 B 中的每一步，我们会在缓存中加载一些新的列，去除一些旧的列。当到达A的下一行时，我们仍旧重新从第一列开始循环。我们不断在缓存中添加和删除同样的数据，即缓存颠簸（cache thrashing）。

如果所有数据均适应缓存，则颠簸不会出现。如果我们处理的是小型矩阵，则它们会舒适地待在缓存里，不用经历重复的驱逐。庆幸的是，我们可以将矩阵相乘分解为子矩阵。要想计算 C 的r×c平铺，我们仅需要A的r行和B的c列。接下来，我们将 C 分解为6x16的平铺：

Code

C(x, y) += A(k, y) * B(x, k);

C.update().tile(x, y, xo, yo, xi, yi, 6, 16)
/*in pseudocode:for xo in 0..N/16:    
for yo in 0..M/6:        
    for yi in 6:            
        for xi in 0..16:                
            for k in 0..K:                    
                C(...) = ...*/

我们将x,y 维度分解为外侧的xo,yo和内侧的xi,yi。我们将为该6x16 block优化micro-kernel（即xi,yi），然后在所有block上运行micro-kernel（通过xo,yo进行迭代）。

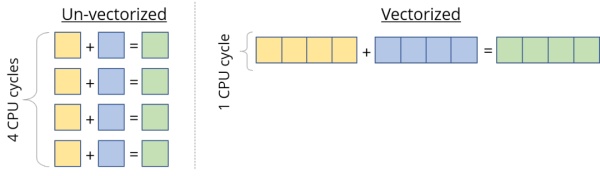
向量化 & FMA

大部分现代CPU支持SIMD（Single Instruction Multiple Data，单指令流多数据流）。在同一个CPU循环中，SIMD可在多个值上同时执行相同的运算/指令（如加、乘等）。如果我们在4个数据点上同时运行SIMD指令，就会直接实现4倍的加速。

因此，当我们计算处理器的峰值速度时，我们其实有些作弊，把该向量化性能作为峰值性能。对于向量等数据而言，SIMD用处多多，在处理此类数据时，我们必须对每一个向量元素执行同样的指令。但是我们仍然需要设计计算核心，以充分利用它。
计算峰值FLOPs时，我们所使用的第二个技巧是FMA（Fused Multiply-Add）。尽管乘和加是两种独立的浮点运算，但它们非常常见，有些专用硬件单元可以将二者融合为一，作为单个指令来执行。编译器通常会管理FMA的使用。
在英特尔CPU上，我们可以使用SIMD（AVX & SSE）在单个指令中处理多达8个浮点数。编译器优化通常能够独自识别向量化的时机，但是我们需要掌控向量化以确保无误。

Code

C.update().tile(x, y, xo, yo, xi, yi, 6, 16).reorder(xi, yi, k, xo, yo).vectorize(xi, 8)
/*in pseudocode:for xo in 0..N/16:    
for yo in 0..M/6:        
    for k in 0..K:            
        for yi in 6:                
            for vectorized xi in 0..16:                    
                C(...) = ...*/

多线程处理（Threading）

到现在为止，我们仅使用了一个CPU内核。我们拥有多个内核，每个内核可同时执行多个指令。一个程序可被分割为多个线程，每个线程在单独的内核上运行。

Code

C.update().tile(x, y, xo, yo, xi, yi, 6, 16).reorder(xi, yi, k, xo, yo).vectorize(xi, 8).parallel(yo)
/*in pseudocode:for xo in 0..N/16 in steps of 16:    
for parallel yo in steps of 6:        
    for k in 0..K:            
        for yi in 6:                
            for vectorized xi in 0..16 in steps of 8:                    
                C(...) = ...*/

你可能注意到，对于非常小的规模而言，性能反而下降了。这是因为工作负载很小，线程花费较少的时间来处理工作负载，而花费较多的时间同步其他线程。多线程处理存在大量此类问题。

展开（Unrolling）

循环使我们避免重复写同样代码的痛苦，但同时它也引入了一些额外的工作，如检查循环终止、更新循环计数器、指针运算等。如果手动写出重复的循环语句并展开循环，我们就可以减少这一开销。例如，不对1个语句执行8次迭代，而是对4个语句执行2次迭代。

这种看似微不足道的开销实际上是很重要的，最初意识到这一点时我很惊讶。尽管这些循环操作可能「成本低廉」，但它们肯定不是免费的。每次迭代2-3个额外指令的成本会很快累积起来，因为此处的迭代次数是数百万。随着循环开销越来越小，这种优势也在不断减小。

展开是几乎完全被编译器负责的另一种优化方式，除了我们想要更多掌控的micro-kernel。

Code

C.update().tile(x, y, xo, yo, xi, yi, 6, 16).reorder(xi, yi, k, xo, yo).vectorize(xi, 8).unroll(xi).unroll(yi)
/*in pseudocode:for xo in 0..N/16:    
for parallel yo:        
    for k in 0..K:            
        C(xi:xi+8, yi+0)            
        C(xi:xi+8, yi+1)            
        ...            
        C(xi:xi+8, yi+5)            
        C(xi+8:xi+16, yi+0)            
        C(xi+8:xi+16, yi+1)            
        ...            
        C(xi+8:xi+16, yi+5)*/

现在我们可以将速度提升到接近60 GFLOP/s。

总结

上述步骤涵盖一些性能加速最常用的变换。它们通常以不同方式组合，从而得到更加复杂的调度策略来计算同样的任务。

下面就是用Halide语言写的一个调度策略：

Code

matrix_mul(x, y) += A(k, y) * B(x, k);    
out(x, y) = matrix_mul(x, y);

out.tile(x, y, xi, yi, 24, 32)        
  .fuse(x, y, xy).parallel(xy)        
  .split(yi, yi, yii, 4)        
  .vectorize(xi, 8)        
  .unroll(xi)        
  .unroll(yii);

 matrix_mul.compute_at(out, yi)        
   .vectorize(x, 8).unroll(y);

 matrix_mul.update(0)        
   .reorder(x, y, k)        
   .vectorize(x, 8)        
   .unroll(x)        
   .unroll(y)        
   .unroll(k, 2);

1. 将out分解为32x24的平铺，然后将每个平铺进一步分解为8x24的子平铺。
2. 使用类似的重排序、向量化和展开，在临时缓冲区（matrix_mul）计算8x24 matmul。
3. 使用向量化、展开等方法将临时缓冲区matrix_mul 复制回out。
4. 在全部32x24平铺上并行化这一过程

参考文章：

通用矩阵乘（GEMM）优化与卷积计算

如何实现高速卷积？深度学习库使用了这些「黑魔法

手推DNN，CNN池化层，卷积层反向传播

额外笔记：

”SAME”和“VALID”

卷积之后的尺寸大小计算公式为：

• input_x (FN,FC,FH,FW)
• 滤波器 Filter大小 (FN,FC,FH,FW)
• Height与width 步长strides S
• Padding size P
• 求输出的shape: (FN,FC,FH,FW)

我们可以得出输出大小

new_height = (input_height - filter_height + 2 * P)/S + 1
new_width = (input_width - filter_width + 2 * P)/S + 1

在实际操作时，我们还会碰到 **padding的两种方式 “SAME” 和 “VALID”，padding = “SAME”时，会在图像的周围填 “0”，padding = “VALID”则不需要，即 P=0。**一般会选“SAME”，以来减缓图像变小的速度，二来防止边界信息丢失

1. padding = “VALID”： P=0
2. padding = “SAME”： kernel_size=1时，P=0；kernel_size=3时，P=1；kernel_size=5时，P=3，以此类推。