过拟合与正则化

过拟合

图1，2：

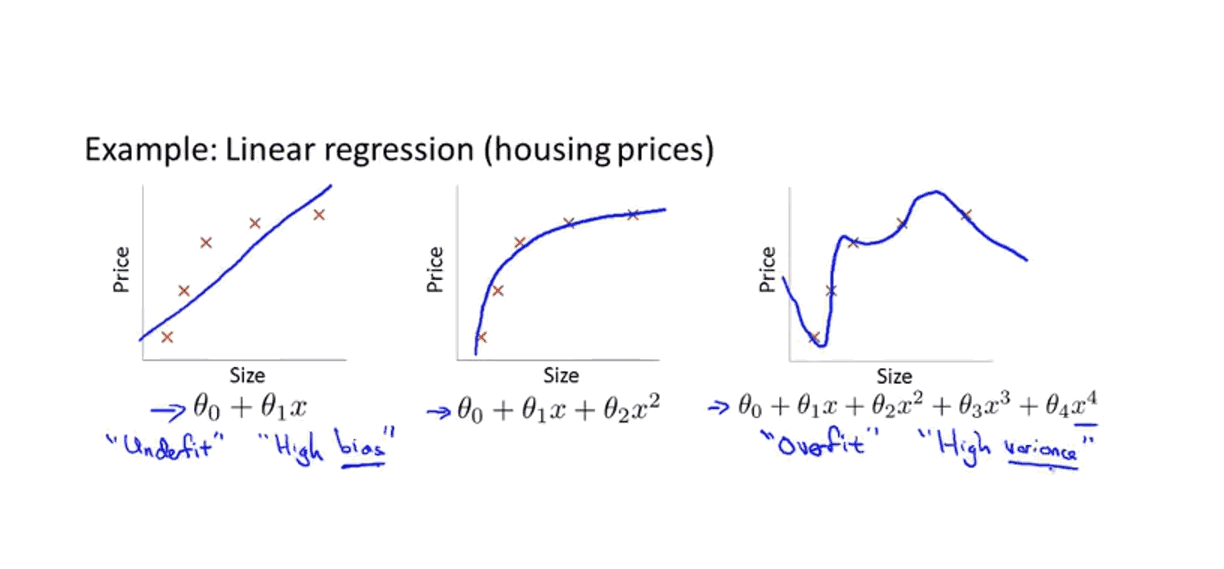
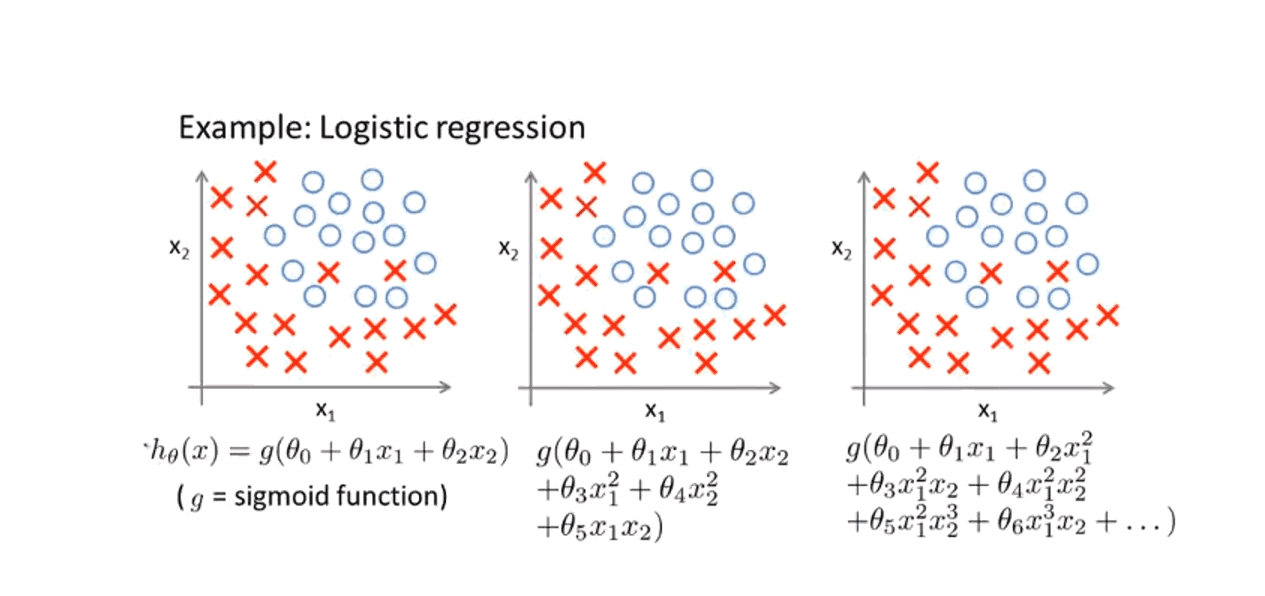
1-3与2-3过拟合，代价函数等于0或者无限接近于0，但无法应用于新样本中.

图3：

当有很多特征变量时，已经不是多项式阶次的选择问题。当我们预测房价时，有许多特征变量与房价可能有关，但是当特征变量过多，训练样本过少时，则容易出现过拟合问题。

为了解决过拟合问题，有两个方法：

1.尽量减少选取变量的数量，如人工检查变量清单，并以此决定哪些变量更为重要，哪些特征变量应该保留，哪些应该舍弃。

这种方法可以有效防止过拟合的发生，缺点;舍弃一部分特征变量也舍弃了关于问题的一些信息。

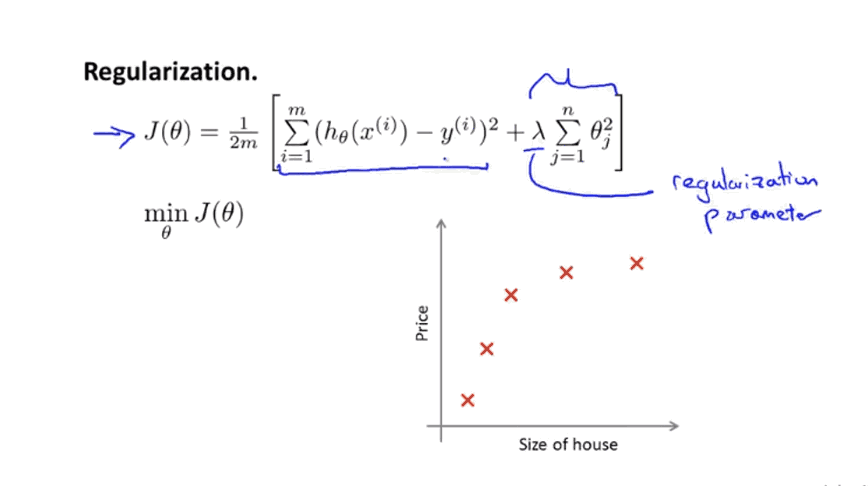
2.正则化：保留所有特征变量但是减小量级$\theta_j$的大小，

正则化

图4：

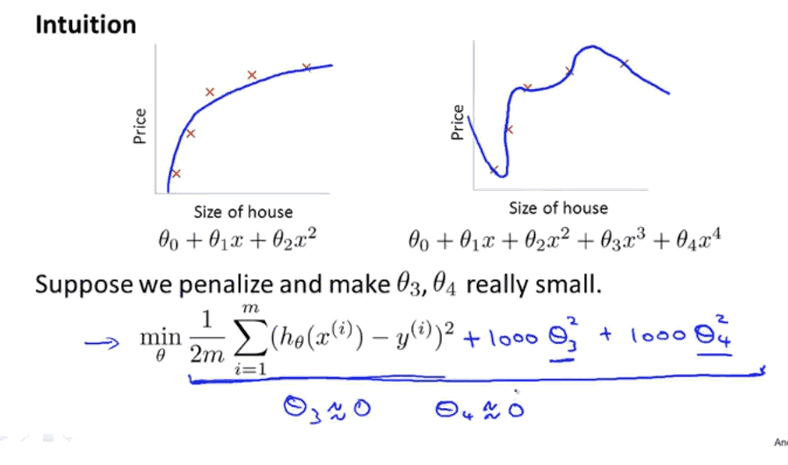
当我们想让这个新函数尽可能小的时候，要使$\theta_3与\theta_4$尽可能小，因为$\theta_3与\theta_4$系数为1000，使整个函数变得非常大，当我们最小化新函数时，我们要使$\theta_3与\theta_4尽可能者接近0$，即消去$\theta_3与\theta_4$，那么这个函数相当于二次函数加上了一些非常小的项。

这就是加入惩罚增大两个参数的结果，即正则化的思想：如果将$\theta_1,\theta_2,\theta_3,\theta_4\theta_5...$都加上惩罚项，这么做就相当于去简化这个假设模型，参数越接近于0.结果表明，这些参数的数值越小，我们得到的函数就越平滑也越简单，越不容易出现过拟合问题，

图5：

在正则化中，修改代价函数（添加正则化项）来缩小所有参数（因为不知该选那些参数去缩小），此处求和从参数$\theta_1$开始没有给参数$\theta_0$添加惩罚项（约定俗成），对结果影响不大。

图6：

$\lambda$作用，控制两个不同目标之间的取舍，第一个目标与函数第一项有关（更好的拟合训练集），第二个目标，保持参数尽量地小（与正则化目标有关）。$\lambda$即正则化参数作用是控制这辆两个目标之间的关系。即更好的拟合训练集和将参数控制的更小，保持假设模型简单避免出现过拟合。

图7:

$\lambda$过大会导致参数都接近于0，相当于只保留了$\theta_0$，用一条直线去拟合数据，导致欠拟合。

L1与L2正则