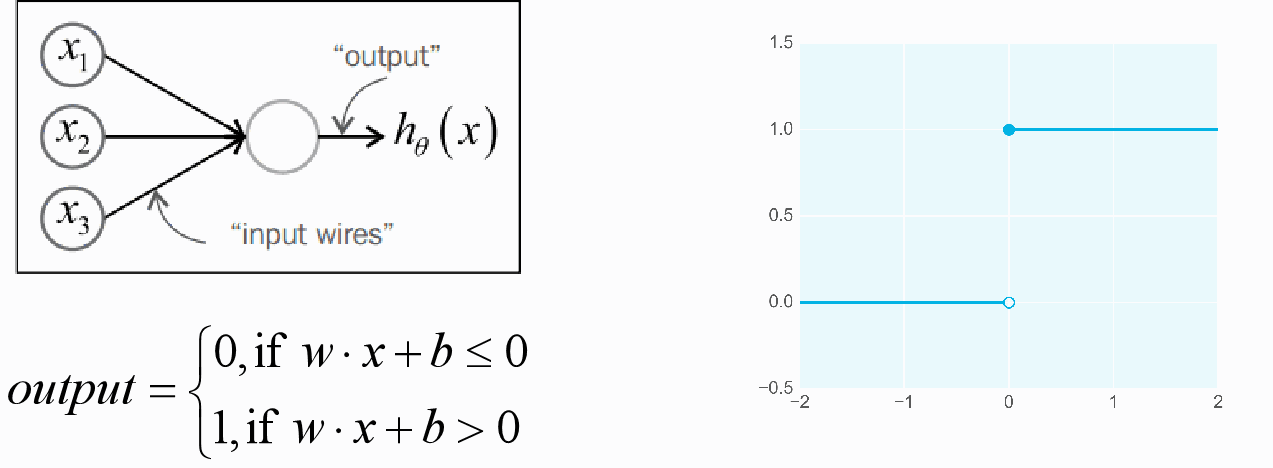
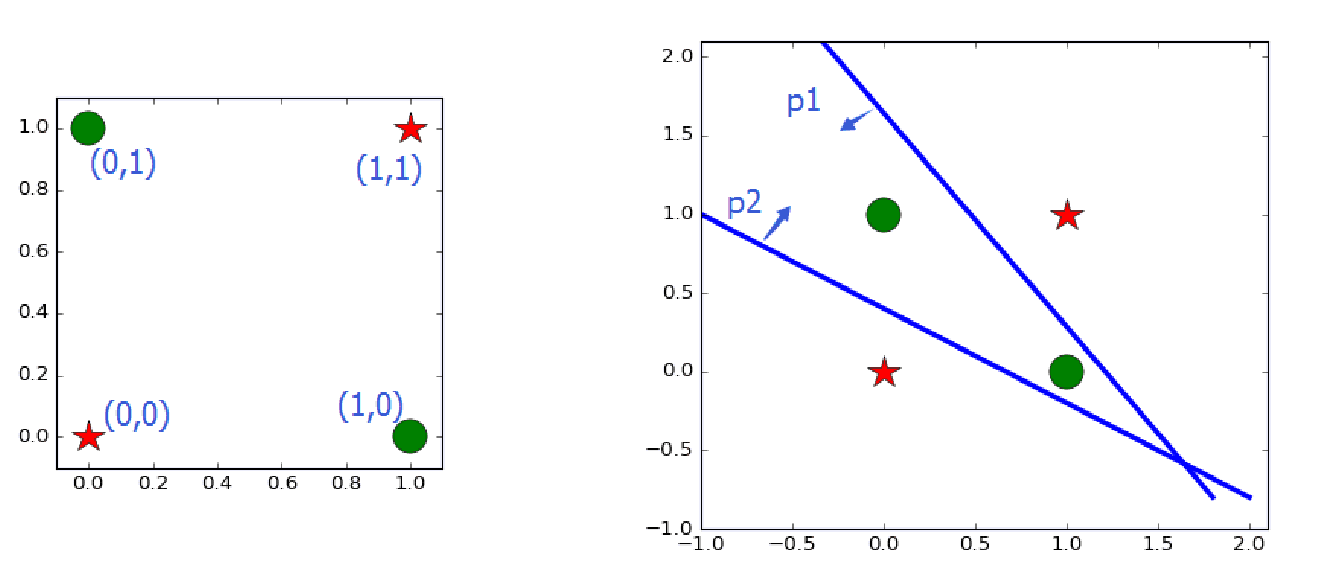
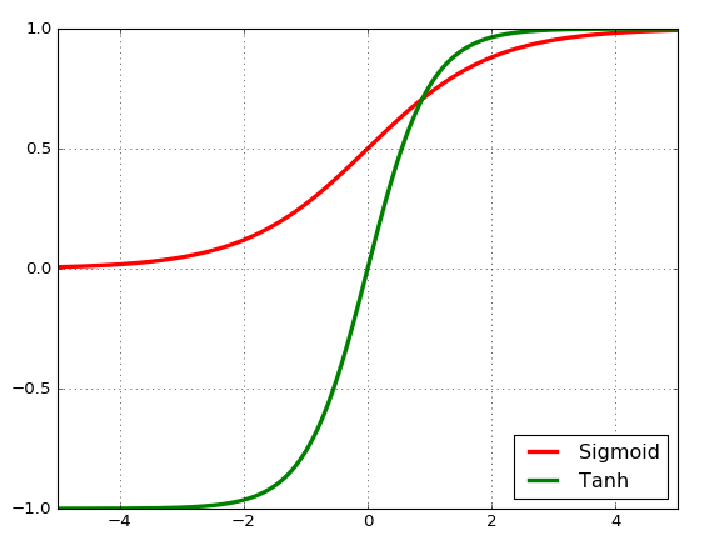
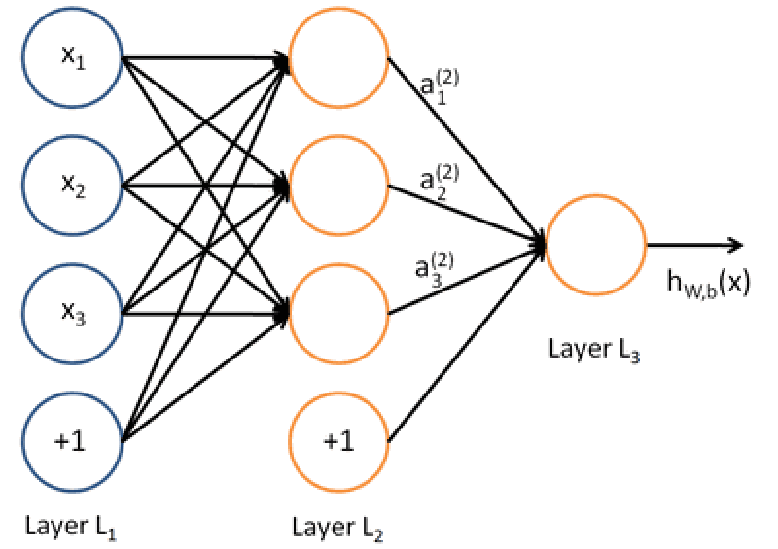
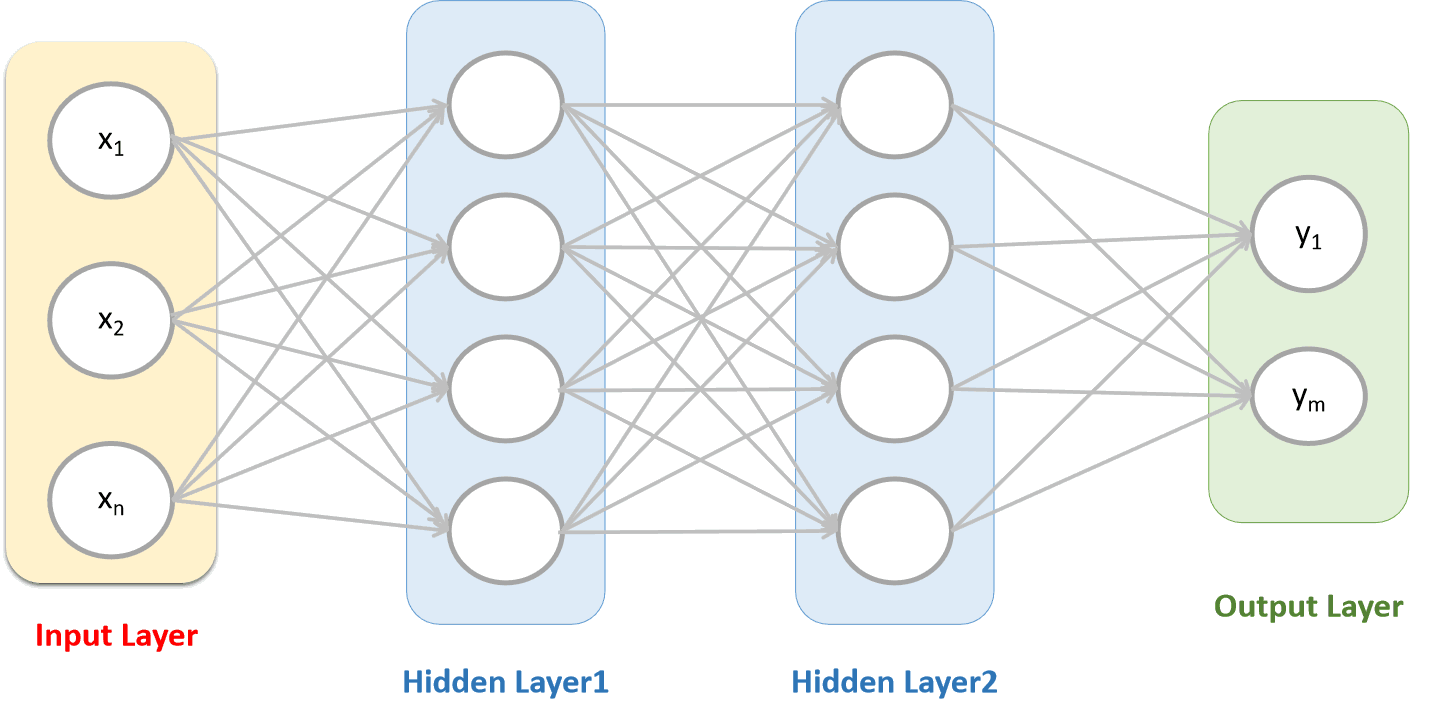
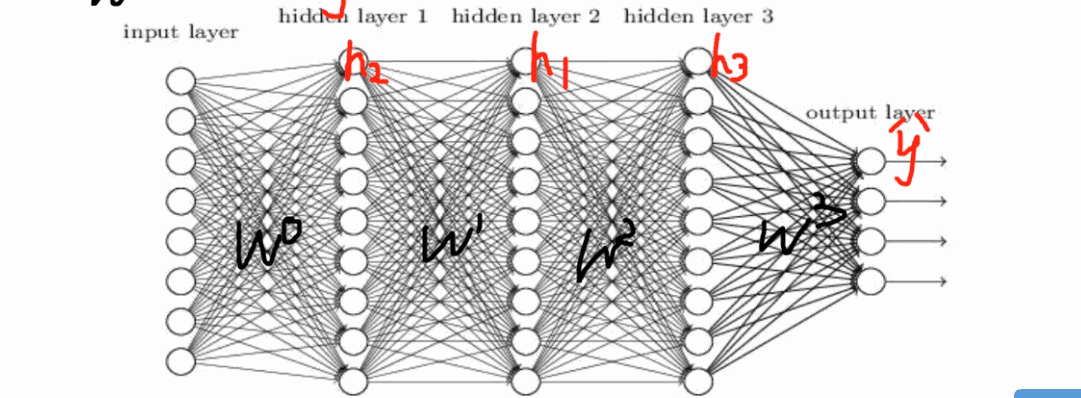
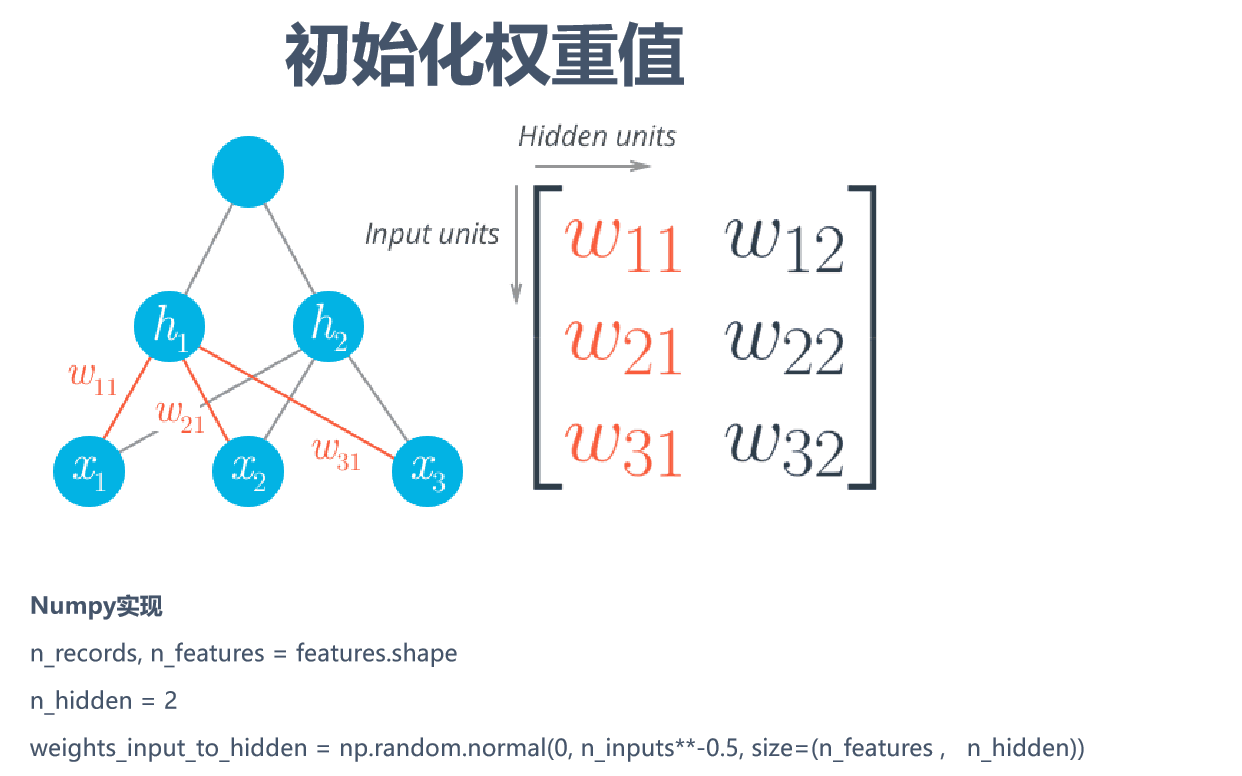
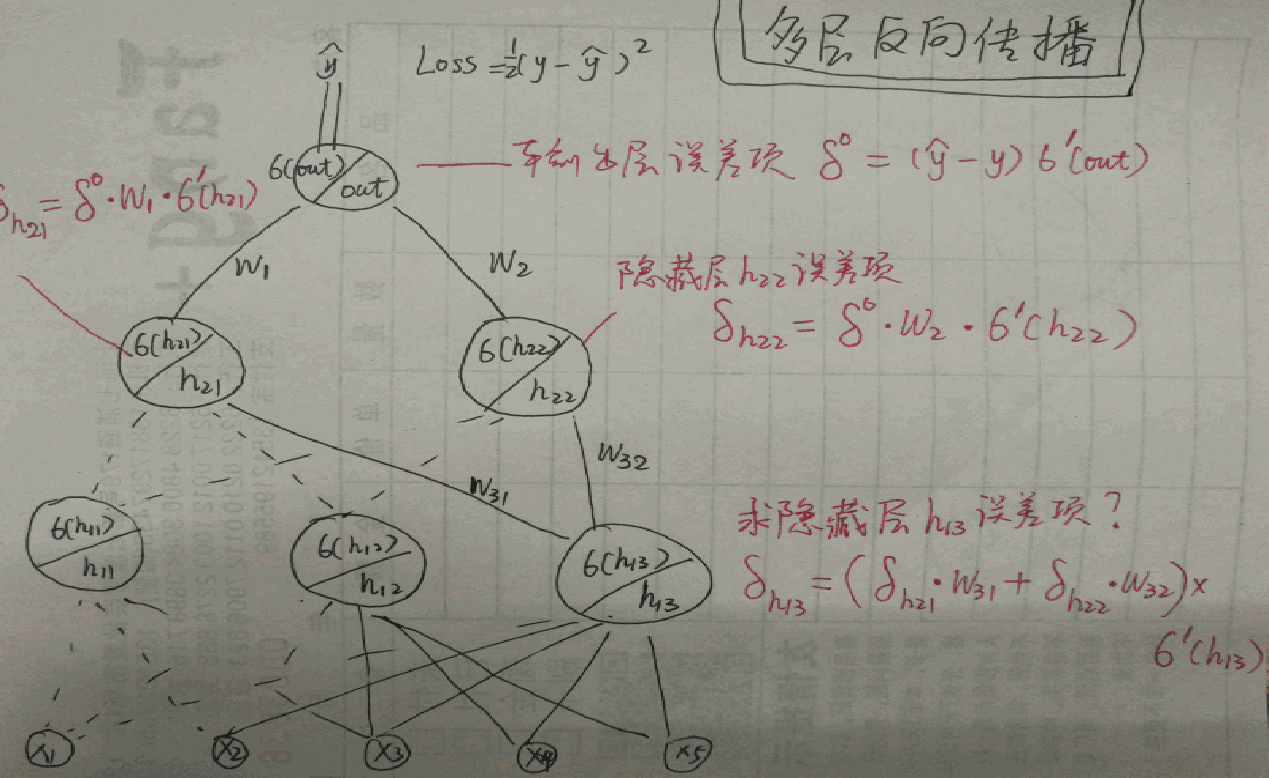
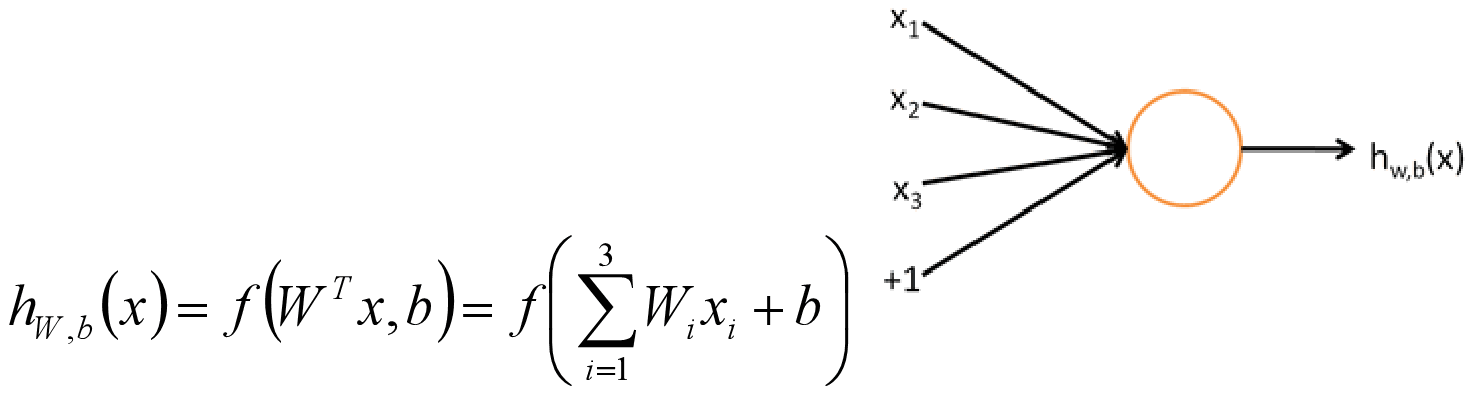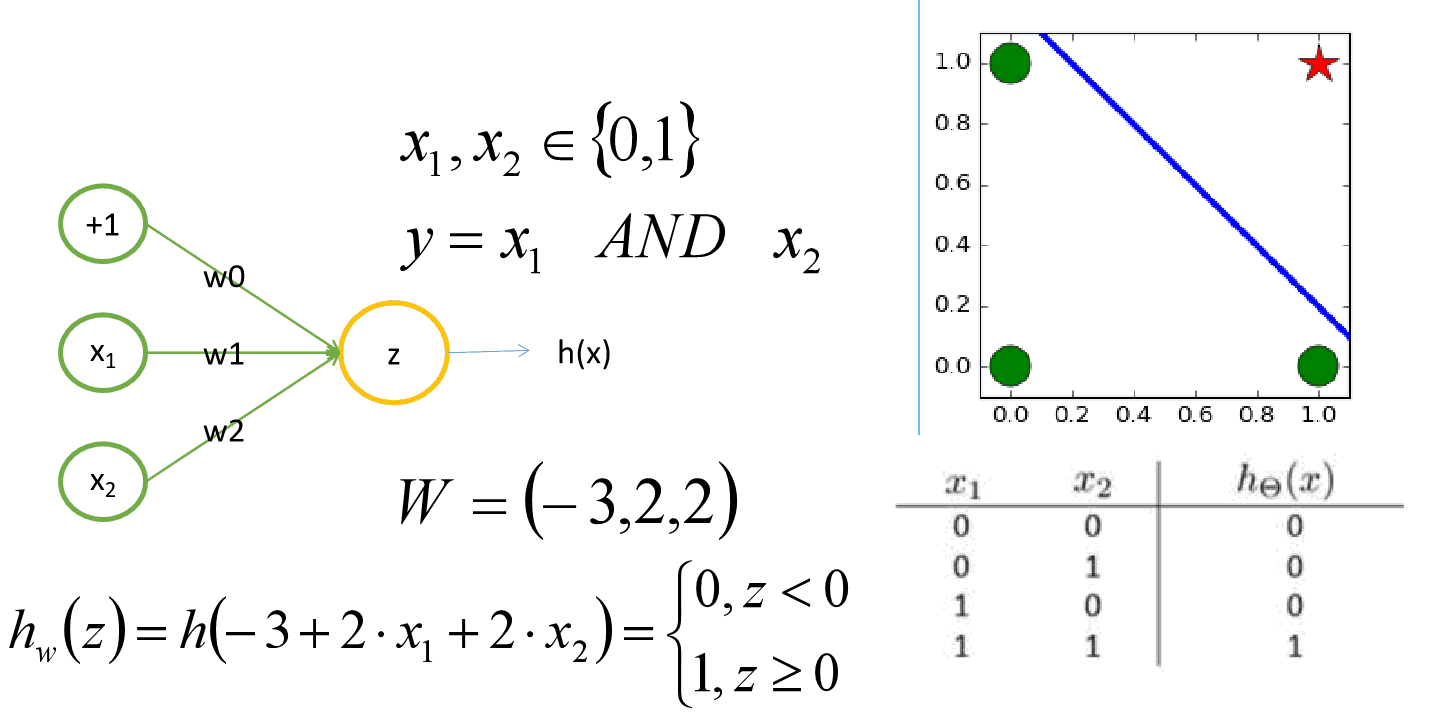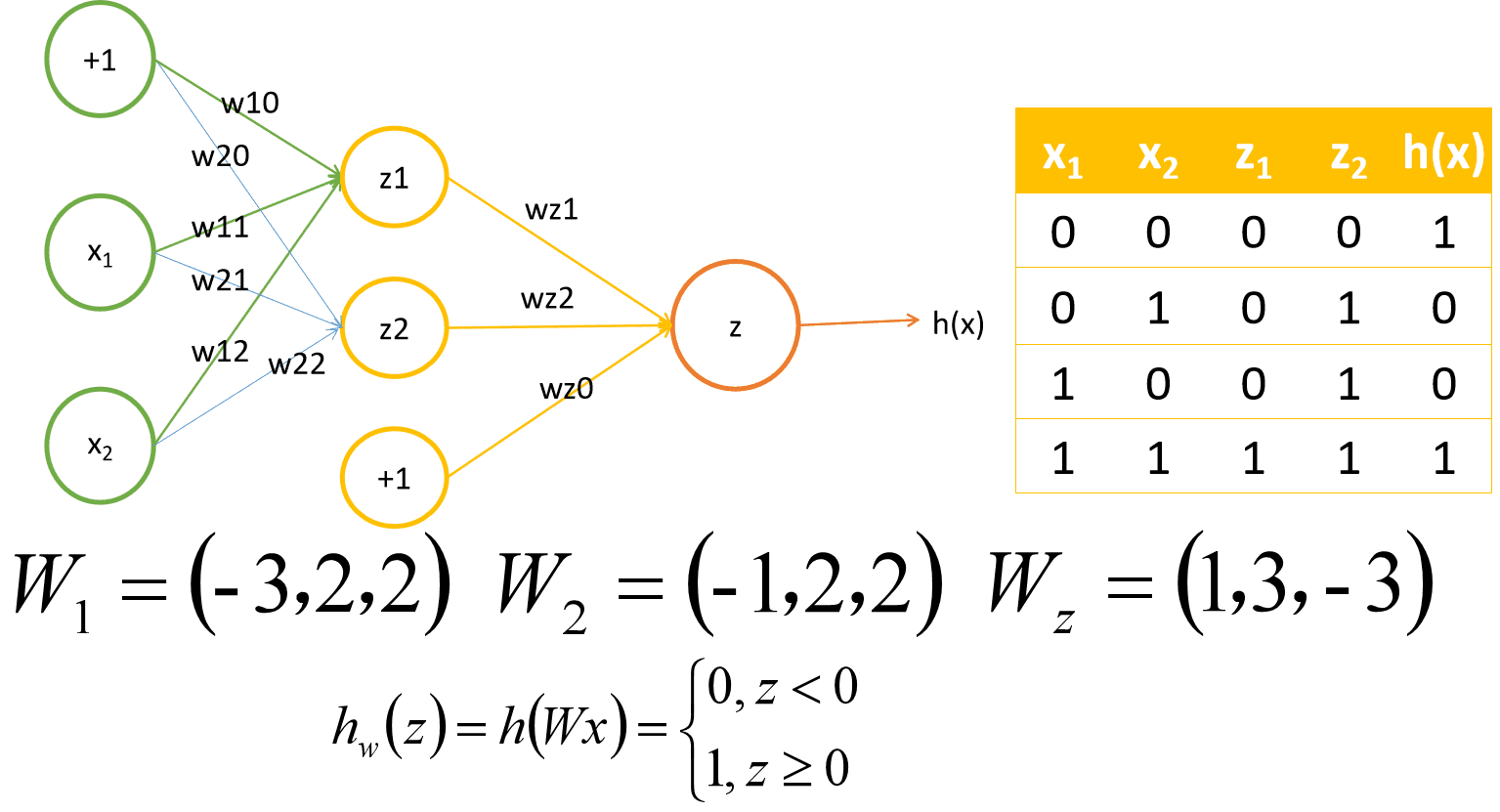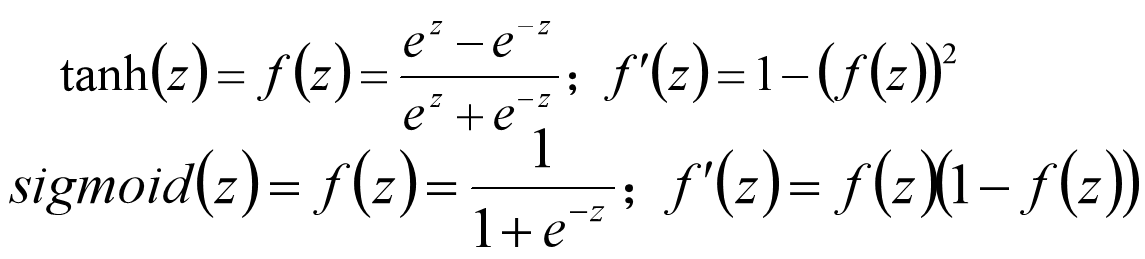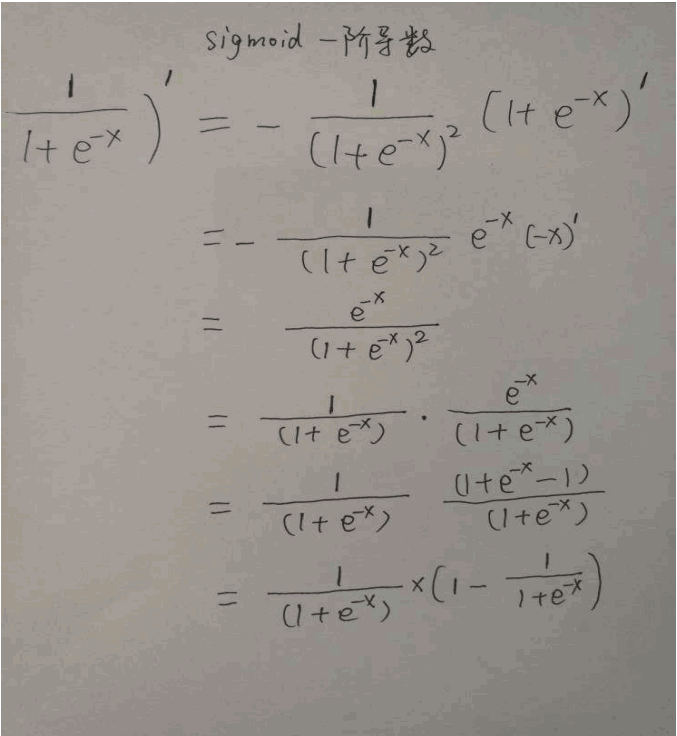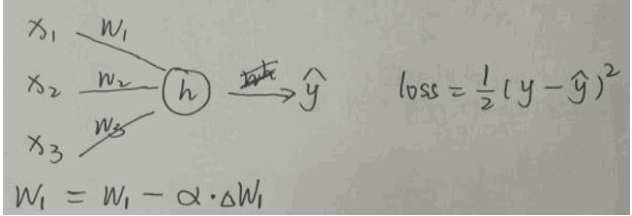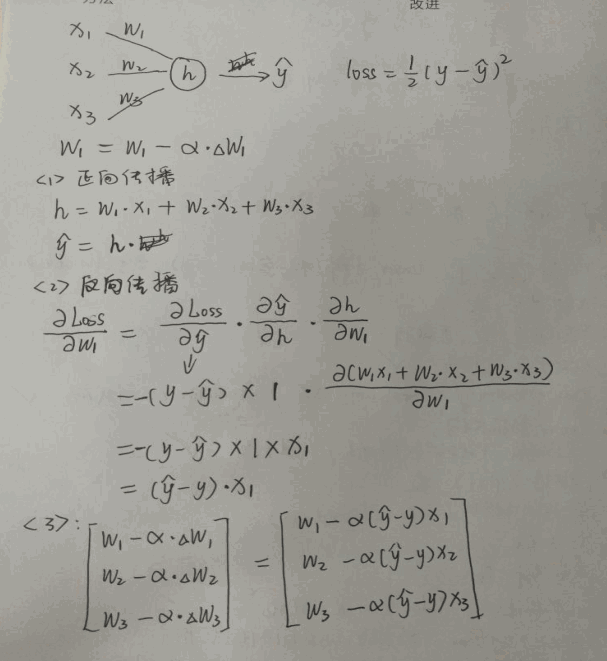小批量梯度下降MBGD 一般选用2的n次方大小
"""
案例:研究生学院录取数据,用梯度下降训练一个网络。
数据有三个输入特征:GRE 分数、GPA 分数和本科院校排名(从 1 到 4)。排名 1 代表最好,排名 4 代表最差。
"""
import numpy as np
import pandas as pd
pd.set_option('display.max_columns', 1000)
pd.set_option('display.width', 1000)
pd.set_option('display.max_colwidth', 1000)
admissions = pd.read_csv('../datas/11.csv')
def data_explore(admissions):
print(admissions.head(n=10))
print(admissions.info()) # 查看是否有空值,以及数据类型
print(admissions.describe()) # 再次可以看到是否有空值,以及值范围,需要考虑做数据变换。
print('各个样本相应的数量为:{}'.format(admissions['admit'].value_counts())) # 查看样本是否均衡
"""
一、数据清理
1、分类变量哑编码
rank 是类别特征,其中的数字并不表示任何相对的值。排名第 2 并不是排名第 1 的两倍;
排名第 3 也不是排名第 2 的 1.5 倍。因此,我们需要用哑变量 来对 rank 进行编码。
把数据分成 4 个新列,用 0 或 1 表示。排名为 1 的行对应 rank_1 列的值为 1 ,其余三列的值为 0;
排名为 2 的行对应 rank_2 列的值为 1 ,其余三列的值为 0,以此类推。
2、连续变量标准化
把 GRE 和 GPA 数据标准化,变成均值为 0,标准偏差为 1。因为 sigmoid 函数会挤压很大或者很小的输入。
很大或者很小输入的梯度为 0,这意味着梯度下降的步长也会是 0。
"""
def data_transform(admissions):
"""
一 rank代表学校等级(1--4),转成哑变量
1、 用pd.get_dummies 将rank列,转成哑变量,新变量名前缀为:prefix='rank'
2、将原数据集admissions 和 1 进行列拼接;
3、drop原始的rank列。
"""
data = pd.concat([admissions, pd.get_dummies(admissions['rank'], prefix='rank')], axis=1)
data = data.drop('rank', axis=1)
"""
二、gre和gpa连续变量的标准化
标准做法:先拆分数据集--使用训练数据集的统计量 去标准化 验证和测试。
"""
for field in ['gre', 'gpa']:
mean, std = data[field].mean(), data[field].std()
data.loc[:, field] = (data[field] - mean) / std
"""
三、数据拆分:分成训练 和 测试数据集
1、设置随机数种子,确保大家执行和我们这里演示的结果一致;
2、使用np.random.choice,随机选择数据集中90% 数据的index
"""
# 随机打乱,并将数据集拆分为 90%训练---10%测试数据集。
np.random.seed(42)
sample = np.random.choice(data.index, size=int(len(data) * 0.9), replace=False)
train_data, test_data = data.iloc[sample], data.drop(sample)
"""
四、 将自变量(features)和目标值分离
"""
features_train, targets_train = train_data.drop('admit', axis=1), train_data['admit']
features_test, targets_test = test_data.drop('admit', axis=1), test_data['admit']
return features_train.values, targets_train.values, features_test.values, targets_test.values
def sigmoid(x):
"""
sigmoid激活函数
:param x:
:return:
"""
return 1/(1+np.exp(-x))
def gre_bp_answer(feature_train, target_train, feature_test, target_test):
# 1、超参数
n_hidden = 2
epochs = 2000
learning_rate = 0.06
# 获取样本数量和 特征数量
n_records, n_features = features_train.shape
last_loss = None
# 2、初始化模型权重
weights_input_2_hidden = np.random.normal(
loc=0.0, scale=0.1, size=[n_features, n_hidden]
)
# weights_hidden_2_output = np.random.normal(
# scale=0.1, size=n_hidden
# )
weights_hidden_2_output = np.random.normal(
scale=0.1, size=[n_hidden, 1]
)
# 构建迭代次数的循环
for e in range(epochs):
# 构建存储梯度值的delta_w
del_weights_input_2_hidden = np.zeros(weights_input_2_hidden.shape)
del_weights_hidden_2_output = np.zeros(weights_hidden_2_output.shape)
for x, y in zip(feature_train, target_train):
# 1、正向传播;
hidden_input = np.matmul(x, weights_input_2_hidden)
hidden_output = sigmoid(hidden_input)
# hidden_output shape = (2,)
final_input = np.matmul(hidden_output, weights_hidden_2_output)
y_hat = sigmoid(final_input) # shape = () 是一个标量
# 2、求误差
error = y_hat - y
# 3、反向传播
# 求输出层误差项
output_error_term = error * y_hat * (1-y_hat) # 标量
# 隐藏层误差
hidden_error = output_error_term * weights_hidden_2_output # (n_hidden,)
# 隐藏层误差项
# print(hidden_error.shape, hidden_output.shape)
hidden_error_term = hidden_error.reshape(-1) * hidden_output *(1-hidden_output)
# (n_hidden,)
del_weights_input_2_hidden += x[:, None] * hidden_error_term
del_weights_hidden_2_output += hidden_output[:, None] * output_error_term
# 更新模型权重
weights_input_2_hidden -= del_weights_input_2_hidden * learning_rate / n_records
weights_hidden_2_output -= del_weights_hidden_2_output * learning_rate / n_records
# 打印模型损失
if e % 100 == 0:
hidden_output = sigmoid(np.dot(features_train, weights_input_2_hidden))
pred_out = sigmoid(np.dot(hidden_output, weights_hidden_2_output))
loss = np.mean((pred_out - target_train)**2)
if last_loss and last_loss < loss:
print('警告:模型损失在上升, Train Loss:{}'.format(loss))
else:
print('Epochs:{} - Train Loss:{}'.format(e, loss))
last_loss = loss
#训练结束,使用测试数据集验证模型准确率
hidden = sigmoid(np.dot(feature_test,weights_input_2_hidden))
test_pred = sigmoid(np.dot(hidden,weights_hidden_2_output))
predictions = test_pred > 0.5
accuracy = np.mean(predictions == target_test)
print("Test Accuray:{:,.5f}".format(accuracy))
def get_batches(feature_train, target_train, batch_size = 32):
"""
构建批量数据的生成器
:param feature_train:
:param target_train:
:param batch_size:
:return:
"""
for ii in range(0,len(feature_train), batch_size):
batch_x = feature_train[ii:ii+batch_size]
batch_y = target_train[ii:ii+batch_size]
yield batch_x,batch_y
def gre_bp_MBGD(feature_train, target_train, feature_test, target_test,batch_size = 128):
"""
使用小批量梯度下降实现GRE
:param feature_train:
:param target_train:
:param feature_test:
:param target_test:
:return:
"""
# 1、超参数
n_hidden = 4
epochs = 2000
learning_rate = 0.06
# 获取样本数量和 特征数量
n_records, n_features = features_train.shape
last_loss = None
# 2、初始化模型权重
weights_input_2_hidden = np.random.normal(
loc=0.0, scale=0.1, size=[n_features, n_hidden]
)
weights_hidden_2_output = np.random.normal(
scale=0.1, size=[n_hidden, 1]
)
# 构建迭代次数的循环
for e in range(epochs):
# 构建存储梯度值的delta_w
# del_weights_input_2_hidden = np.zeros(weights_input_2_hidden.shape)
# del_weights_hidden_2_output = np.zeros(weights_hidden_2_output.shape)
for batch_x, batch_y in get_batches(feature_train, target_train, batch_size):
# 1、正向传播;
hidden_input = np.matmul(batch_x, weights_input_2_hidden)
hidden_output = sigmoid(hidden_input)
# hidden_output shape = (2,)
final_input = np.matmul(hidden_output, weights_hidden_2_output)
y_hat = sigmoid(final_input) # shape = () 是一个标量
# 2、求误差
error = y_hat - batch_y[:,None] #[N,1]
# 3、反向传播
# 求输出层误差项 [N,1]
output_error_term = error * y_hat * (1-y_hat) # 标量
# 隐藏层误差[N,4]
hidden_error = np.matmul(output_error_term , weights_hidden_2_output.transpose()) # (n_hidden,)
# 隐藏层误差项
# print(hidden_error.shape, hidden_output.shape)
hidden_error_term = hidden_error * hidden_output *(1-hidden_output)
# (n_hidden,)
del_weights_input_2_hidden =np.matmul(np.transpose(batch_x),hidden_error_term)/batch_size
del_weights_hidden_2_output = np.matmul(np.transpose(hidden_output),output_error_term)/batch_size
# 更新模型权重
weights_input_2_hidden -= del_weights_input_2_hidden * learning_rate / n_records
weights_hidden_2_output -= del_weights_hidden_2_output * learning_rate / n_records
# 打印模型损失
if e % 100 == 0:
hidden_output = sigmoid(np.dot(features_train, weights_input_2_hidden))
pred_out = sigmoid(np.dot(hidden_output, weights_hidden_2_output))
loss = np.mean((pred_out - target_train)**2)
if last_loss and last_loss < loss:
print('警告:模型损失在上升, Train Loss:{}'.format(loss))
else:
print('Epochs:{} - Train Loss:{}'.format(e, loss))
last_loss = loss
#训练结束,使用测试数据集验证模型准确率
hidden = sigmoid(np.dot(feature_test,weights_input_2_hidden))
test_pred = sigmoid(np.dot(hidden,weights_hidden_2_output))
predictions = test_pred > 0.5
accuracy = np.mean(predictions == target_test)
print("Test Accuray:{:,.5f}".format(accuracy))
def get_batches(feature_train, target_train, batch_size = 32):
"""
构建批量数据的生成器
:param feature_train:
:param target_train:
:param batch_size:
:return:
"""
for ii in range(0,len(feature_train), batch_size):
batch_x = feature_train[ii:ii+batch_size]
batch_y = target_train[ii:ii+batch_size]
yield batch_x,batch_y
if __name__ == '__main__':
# data_explore(admissions)
features_train, targets_train, features_test, targets_test = data_transform(admissions)
#print(features_train[:,None])
gre_bp_answer(features_train, targets_train, features_test, targets_test)
gre_bp_MBGD(features_train, targets_train, features_test, targets_test, batch_si
|