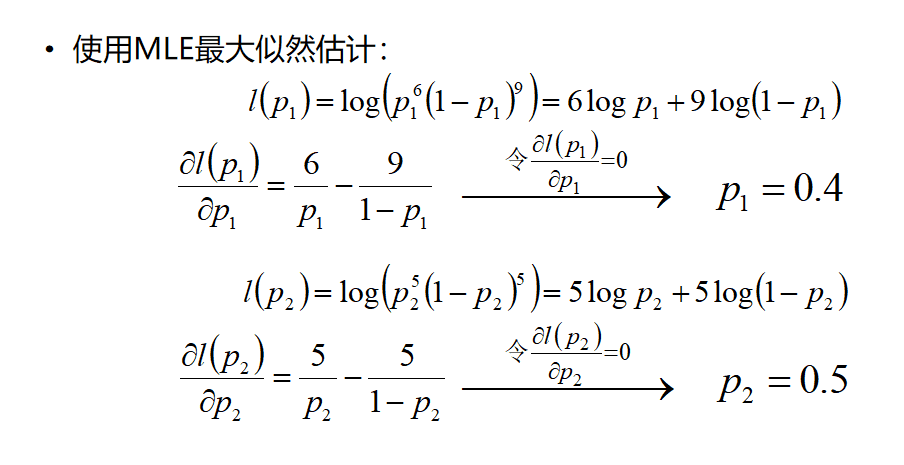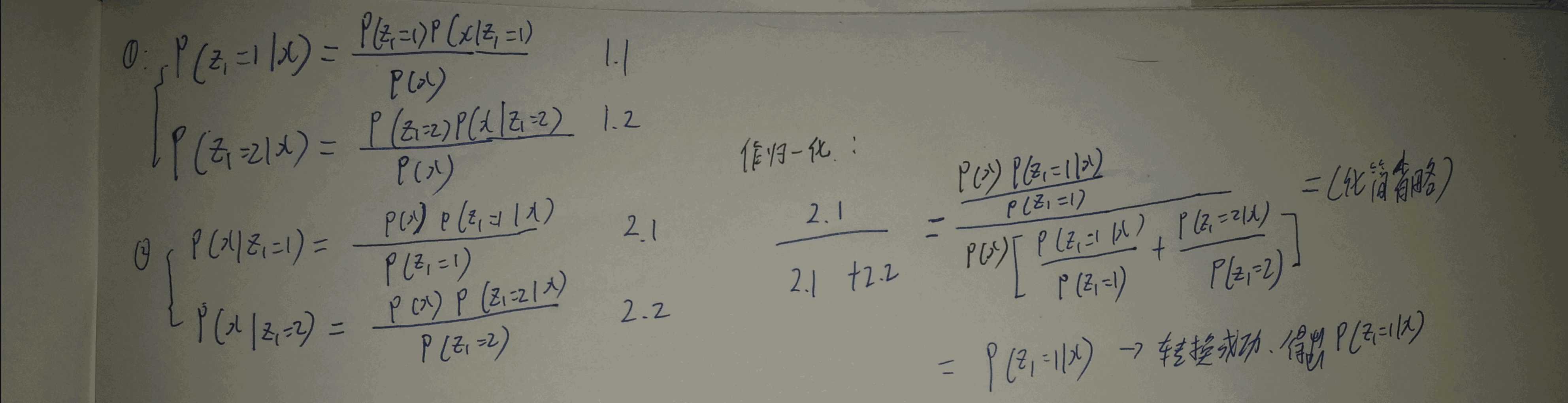数学公式：

Jensen不等式

如果函数f为凸函数，那么存在下列公式： $f(\theta x_1 +(1-\theta x_2))\leq \theta f(x_1)+(1-\theta)f(x_2)$

若 $\theta_1,\theta_2,...\theta_n\geq0,\theta_1+\theta_2+...+\theta_n=1$ ，则 $f(\theta_1x_1+\theta_2x_2+...+\theta_nx_n)\leq\theta_1f(x_1)+\theta_2f(x_2)+...+\theta_nf(x_n)$ ,则f((E(x))≤E(f(x))

特别地，如果函数 f(x)是严格凸函数，当且仅当p(x=E(x))=1,即随机变量是常量时等号成立。 $f(\theta x_1 +(1-\theta x_1))=\theta f(x_1)+(1-\theta)f(x_1)=f(x_1)$

EM算法

EM算法(Expectation Maximization Algorithm, 最大期望算法)是一种迭代类型的算法，是一种在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量。

EM算法流程：

1.初始化分布参数/模型参数

2.重复下列两个操作直到收敛：

E步骤：估计隐藏变量的概率分布期望函数；
M步骤：根据期望函数重新估计分布参数。

EM算法原理

给定的m个训练样本{x(1),x(2),…,x(m)}，样本间独立，找出样本的模型参数θ，极大化模型分布的对数似然函数如下：

${\underset {\theta}{\operatorname {arg\,max} }}\,\sum_{i=1}^{m}{log(P(x^{i};\theta))}$

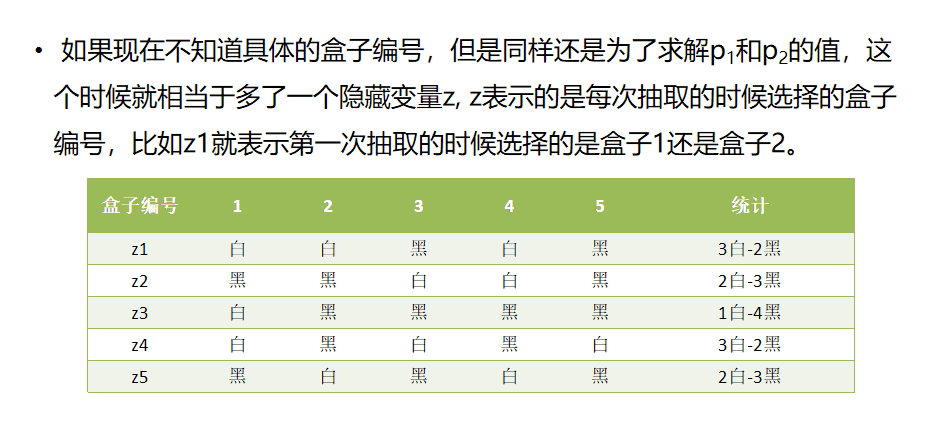
假定样本数据中存在隐含数据z={z(1),z(2),…,z(k)}，此时极大化模型分布的对数似然函数如下：

$\theta=arg\max_{\theta}L({\theta})=arg\max_{\theta}\sum_{i=1}^{m}{log(P(x^{i};\theta))} \\　　　　　　　　　=arg\max_{\theta}\sum_{i=1}^{m}{log(\sum_{z^(i)}{P(z^{i})P(x^{(i)}|z^{i});\theta})} \\　　　　　　=arg\max_{\theta}\sum_{i=1}^{m}{log(\sum_{z^(i)}{P(x^{(i)},z^{i});\theta})}$

令z的分布为Q(z;θ) ，并且Q(z;θ)≥0；那么有如下公式：

$Ｌ(\theta)=\sum_{i=1}^{m}{log\sum_{z}^{}{P(x,z;\theta)}}\\ 　　　　　　=\sum_{i=1}^{m}{log \sum_{z}^{}{Q(z;\theta ^{old})\frac{P(x,z;\theta)}{Q(z;\theta^{old})}}}\\ 　　　　=\sum_{i=1}^{m}{log(E_Q( \frac{P(x,z;\theta)} {Q(z;\theta^{old})} ))}\\ 　　　　\geq \sum_{i=1}^{m}{E_Q(log( \frac{P(x,z;\theta)} {Q(z;\theta^{old} )} ))} \\　　　　　　　=\sum_{a}^{b}{\sum_{z}^{}{ Q(z;\theta^{old} ) log( \frac{P(x,z;\theta^{}{})} {Q(z;\theta^{old} )} ) }}$

公式(2)详解：

1.公式(1)得出的结论理论上可行，实践起来不成。主要是因为似然函数有“和的log”这一项，（公式（2）的前两步）log里面是一个和的形式，一求导这画面不要太美，直接强来你要面对 “两个正态分布的概率密度函数相加”做分母，“两个正态分布分别求导再相加”做分子的分数形式。m个这玩意加起来令它等于0，要求出关于θ的解析解，你对自己的数学水平想的不要太高

2.引入Jensen不等式:X是一个随机变量，f(X)是一个凸函数（二阶导数大或等于0），那么有：E(f(x))≥f(E(x))，当且仅当X是常数的时候等号成立，如果f（X）是凹函数，不等号反向。

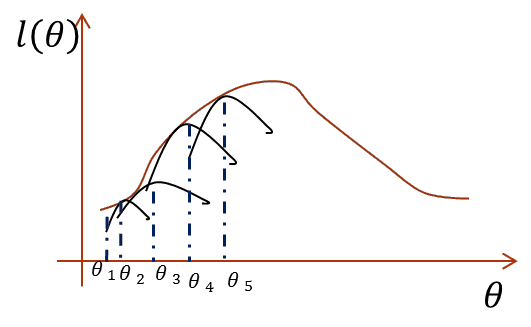
3.直接最大化似然函数做不到，那么如果我们能找到似然函数的一个紧的下界一直优化它，并保证每次迭代能够使总的似然函数一直增大，其实也是一样的。怎么说？画个图你就明白了：

横坐标是参数，纵坐标是似然函数，首先我们初始化一个θ1，根据它求似然函数一个紧的下界，也就是图中第一条黑短线，黑短线上的值虽然都小于似然函数的值，但至少有一点可以满足等号（所以称为紧下界），最大化小黑短线我们就hit到至少与似然函数刚好相等的位置，对应的横坐标就是我们的新的θ2，如此进行，只要保证随着θ的更新，每次最大化的小黑短线值都比上次的更大，那么算法收敛，最后就能最大化到似然函数的极大值处。

来到公式2最后两步骤，我们找到了似然函数的一个下界，那么优化它是否就可以呢？不是的，上面说了必须保证这个下界是紧的，也就是至少有点能使等号成立。由Jensen不等式，等式成立的条件是随机变量是常数，具体到这里，就是：

根据Jensen不等式的特性，当下列式子的值为常数的时候，L(θ)函数才能取等号。

$\\　　　　　　　\frac{P(x,z;\theta^{old})} {Q(z;\theta^{old} )} =c,\forallｘ．\forallｚ$

$Ｑ(z,\theta^{old}) =\frac{P(x,z;\theta^{old})} {c}\\　　　　　　　　　　　　　=\frac{P(x,z;\theta^{old})}{c\cdot \sum_{z^i}^{} {Q(z^i;\theta^{old})}}　　　　　　　　　 \sum_{z^i}^{} {Q(z^i;\theta^{old})}=1\\=\frac{P(x,z;\theta^{old})}{ \sum_{z^i}^{} {c\cdot Q(z^i;\theta^{old})}}　　\\ =\frac{P(x,z;\theta^{old})}{ \sum_{z^i}^{} {P(x,z^i;\theta^{old})}}　\\ =\frac{P(x,z;\theta^{old})}{ P(x;\theta^{old})}\\ =P(z|x;\theta^{old})$

则可得：

$\theta=arg\max_{\theta}Ｌ(\theta)=arg\max_{\theta} \sum_{i=1}^{m}{} \sum_{z}^{}{Q(z;\theta^{old})}log(\frac{P(x,z;\theta^{})}{Q(z;\theta^{old})}) \\ =arg\max_{\theta} \sum_{i=1}^{m}{} \sum_{z}^{}{P(z|x;\theta^{old}log(\frac{P(x,z;\theta^{}}{P(z|x;\theta^{old})}))} \\ \simeq arg\max_{\theta} \sum_{i=1}^{m}{} \sum_{z}^{}{P(z|x;\theta^{old})log(P(x,z;\theta^{}))}$

此处我们化简去loga-logb中的logb,logb此处为常数

EM算法总结：

条件：样本数据x={x1,x2,…,xm}，联合分布p(x,z;θ)，条件分布p(z|x;θ)，最大迭代次数J

随机初始化模型参数θ的初始值θ0
开始EM算法的迭代处理：
E步：计算联合分布的条件概率期望

$Q^j=[(z|x;\theta^j) \\ L(\theta)=\sum_{i=1}^{m}{}\sum_{z}^{}{Q^jlog(P(x,z;\theta))}$

M步：极大化L函数，得到θj+1

$\theta^{j+1}=arg\max_{\theta}L(\theta)$

如果θj+1已经收敛，则算法结束，输出最终的模型参数θ，否则继续迭代处理。

EMs算法收敛性证明

EM算法举例

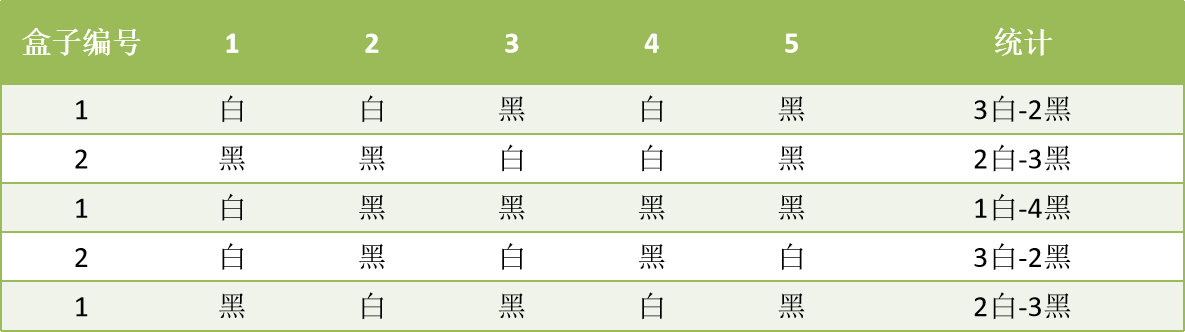
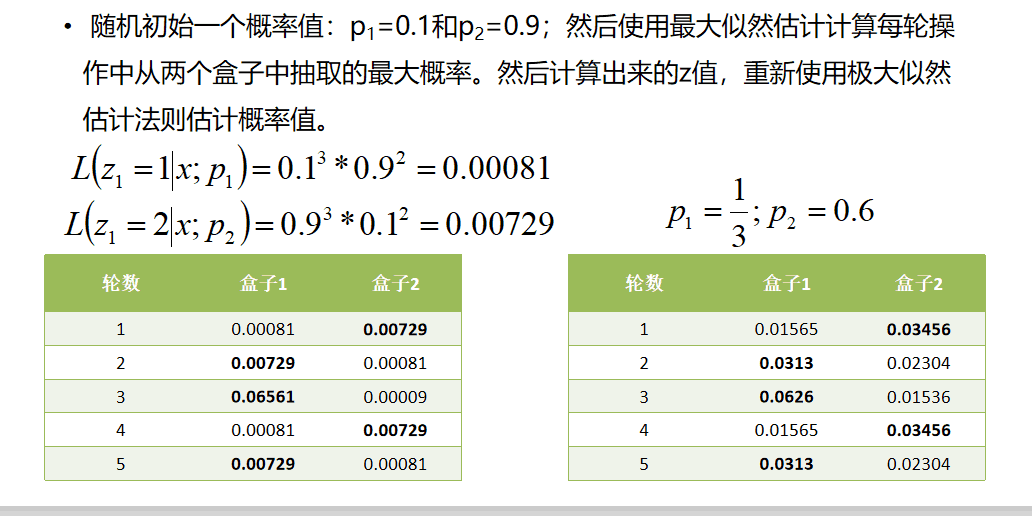
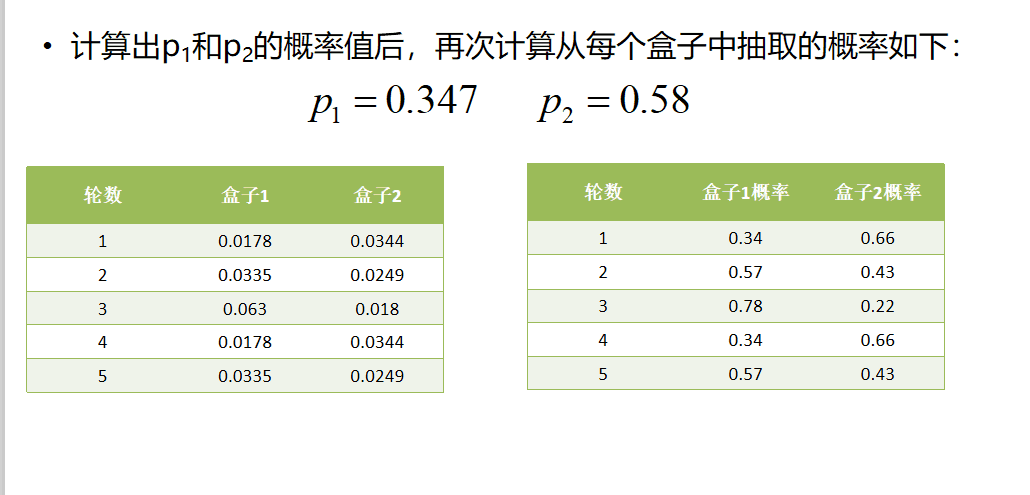
假设现有两个装有不定数量黑球、白球的盒子，随机从盒子中抽取出一个白球的概率分布为p1和p2；为了估计这两个概率，每次选择一个盒子，有放回的连续随机抽取5个球，记录如下：

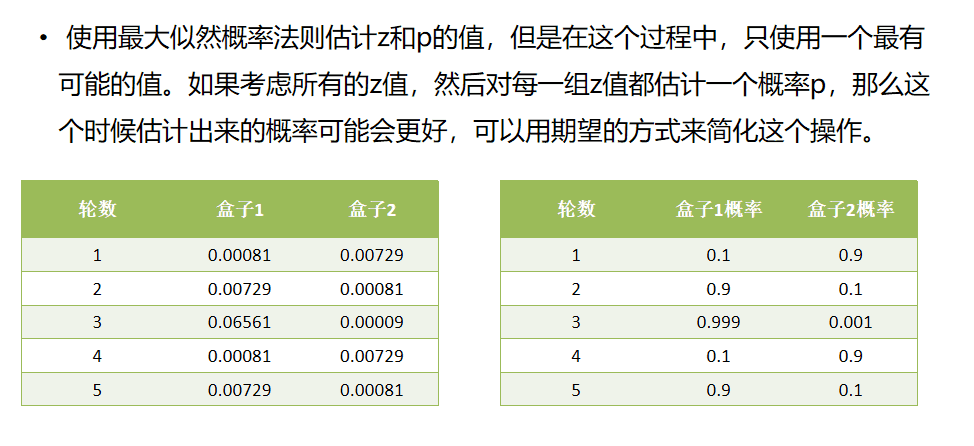
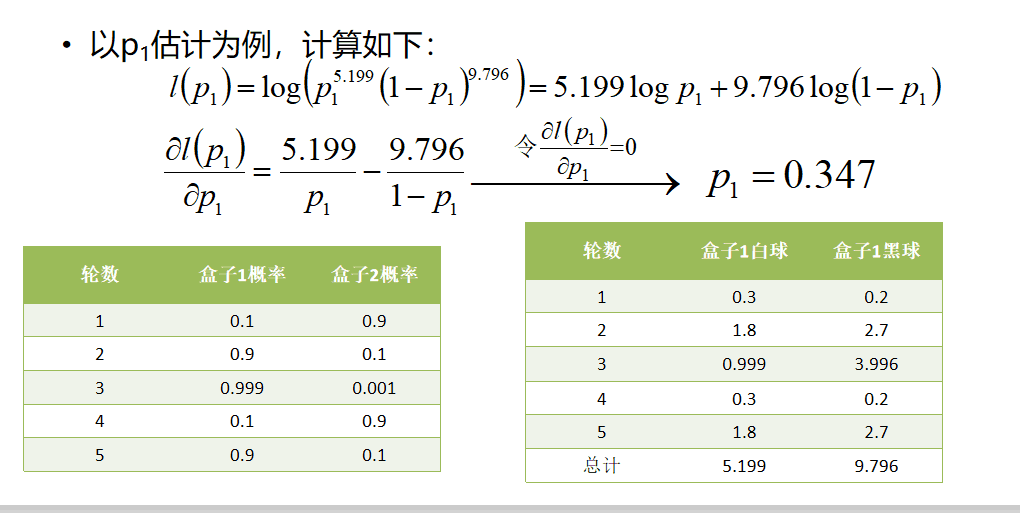
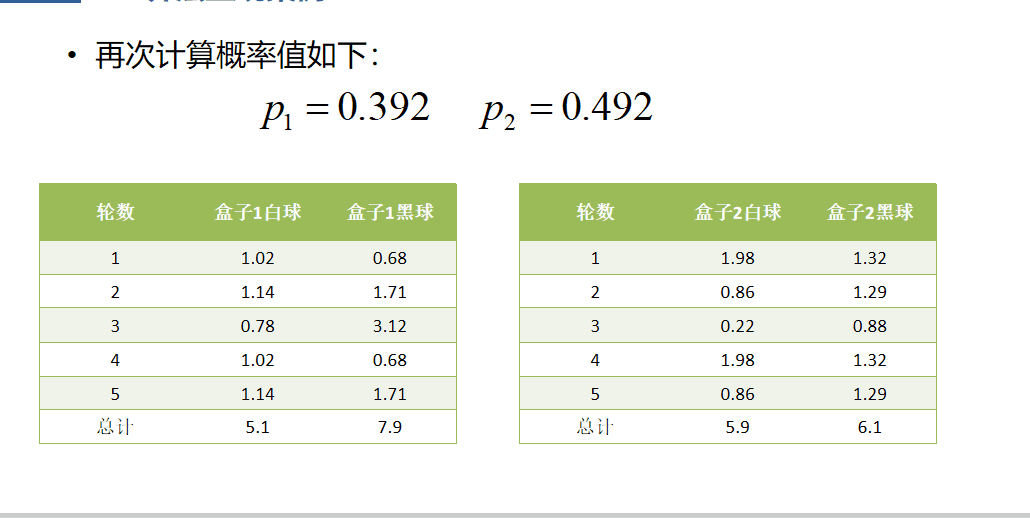
求解过程看如下推导:

EM算法收敛性证明

详见PPT

GMM算法

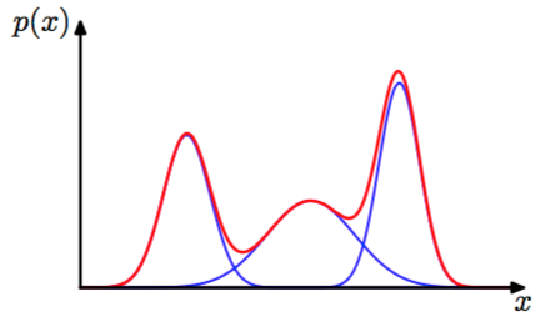
GMM(Gaussian Mixture Model, 高斯混合模型)是指该算法由多个高斯模型线性叠加混合而成。每个高斯模型称之为component。GMM算法描述的是数据的本身存在的一种分布。
GMM算法常用于聚类应用中，component的个数就可以认为是类别的数量。
假定GMM由k个Gaussian分布线性叠加而成，那么概率密度函数如下： $p(x)=\sum_{k=1}^{K}{p(k)p(x|k)}=\sum_{k=1}^{K}{π_kp(x;\mu_k,{\sum_{}^{}{}}_k)}$

此处 $π_k$ 是符号， $\mu_k,{\sum_{}^{}{}}_k$ 代表均值与协方差矩阵

参考链接

[【机器学习】EM算法详细推导和讲解](https://www.cnblogs.com/bigmoyan/p/4550375.html)