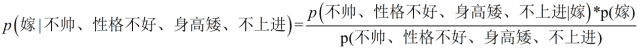涉及公式
先验概率P(A):在不考虑任何情况下,A事件发生的概率
条件概率P(B|A):A事件发生的情况下,B事件发生的概率:
后验概率P(A|B):在B事件发生之后,对A事件发生的概率的重新评估
全概率:如果A和A’构成样本空间的一个划分,那么事件B的概率为:A和A’的概率分别乘以B对这两个事件的概率之和。
A1无依赖,A2依赖于A1,A3依赖于A1A2
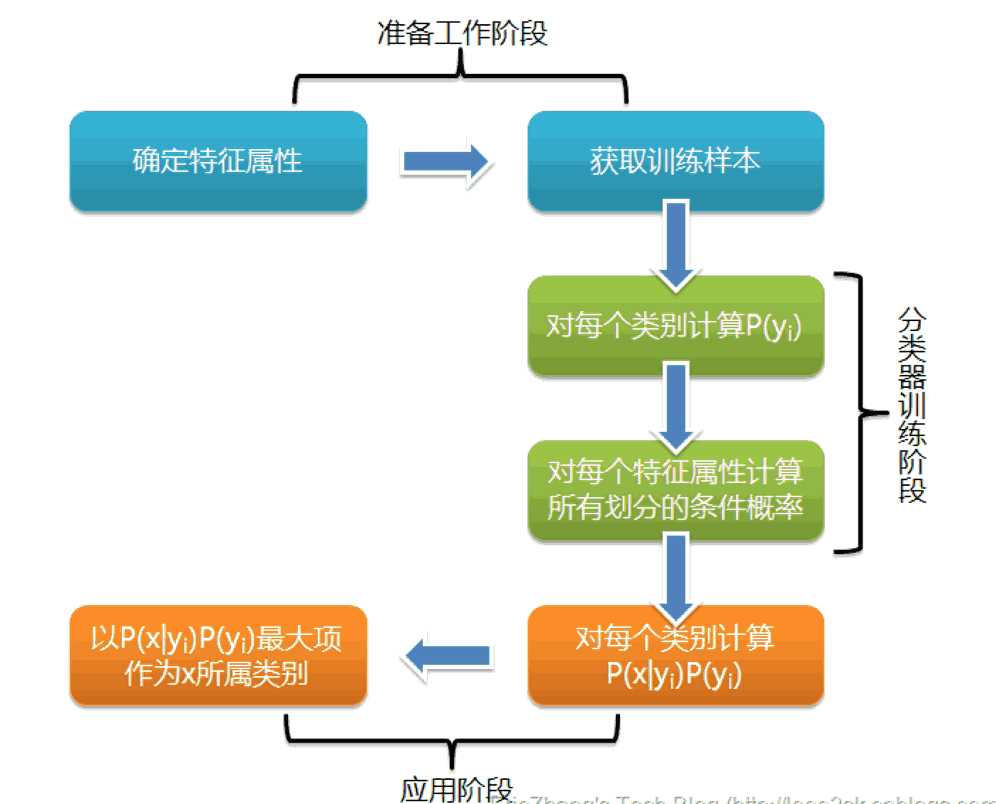
朴素贝叶斯算法
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
分类问题综述
从数学角度来说,分类问题可做如下定义:已知集合
确定映射规则y=f(),使得任意**有且仅有一个**使得成立
其中C叫做类别集合,其中每一个元素是一个类别,而I叫做项集合(特征集合),其中每一个元素是一个待分类项,f叫做分类器。分类算法的任务就是构造分类器f。
分类算法的内容是要求给定特征,让我们得出类别,这也是所有分类问题的关键。那么如何由指定特征,得到我们最终的类别,也是我们下面要讲的,每一个不同的分类算法,对应着不同的核心思想。
朴素贝叶斯分类
那么既然是朴素贝叶斯分类算法,它的核心算法又是什么呢?
是下面这个贝叶斯公式:
换个表达形式就会明朗很多,如下:
我们最终求的p(类别|特征)即可!就相当于完成了我们的任务。
例题分析
下面我先给出例子问题。
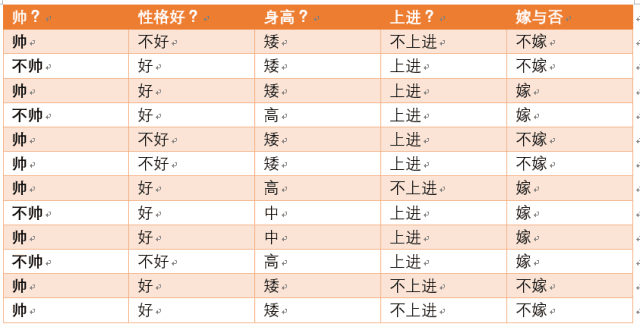
给定数据如下:
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)(至于为什么能求,后面会讲,那么就太好了,将待求的量转化为其它可求的值,这就相当于解决了我们的问题!)
朴素贝叶斯算法的朴素一词解释
那么这三个量是如何求得?
是根据已知训练数据统计得来,下面详细给出该例子的求解过程。
回忆一下我们要求的公式如下:
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!
对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
但是为什么需要假设特征之间相互独立呢?
1、我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
24个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
2、假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),
我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
好的,上面我解释了为什么可以拆成分开连乘形式。那么下面我们就开始求解!
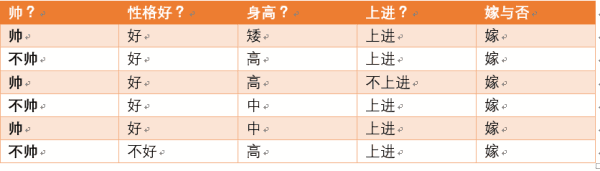
下面我将一个一个的进行统计计算(在数据量很大的时候,根据中心极限定理,频率是等于概率的,这里只是一个例子,所以我就进行统计即可)。
p(嫁)=?
则 p(嫁) = 6/12(总样本数) = 1/2
p(不帅|嫁) = 3/6 = 1/2
则p(性格不好|嫁)= 1/6
p(矮|嫁) = 1/6**
p(不上进|嫁) = 1/6**
下面开始求分母,p(不帅),p(性格不好),p(矮),p(不上进)
不帅统计占4个,那么p(不帅)= 4/12 = 1/3
性格不好占4个,那么p(性格不好) = 4/12 = 1/3
身高矮统计,占7个,那么p(身高矮) = 7/12
不上进统计所示,占4个,那么p(不上进) = 4/12 = 1/3
到这里,要求p(不帅、性格不好、身高矮、不上进|嫁)的所需项全部求出来了,下面我带入进去即可,
= (1/21/61/61/61/2)/(1/31/37/12*1/3)
下面我们根据同样的方法来求p(不嫁|不帅,性格不好,身高矮,不上进),完全一样的做法,为了方便理解,我这里也走一遍帮助理解。首先公式如下:
下面我也一个一个来进行统计计算,这里与上面公式中,分母是一样的,于是我们分母不需要重新统计计算!
p(不嫁)=6/12 = 1/2
p(不帅|不嫁) = 1/6
p(性格不好|不嫁) =3/6 = 1/2
p(矮|不嫁) = 6/6 = 1
p(不上进|不嫁) = 3/6 = 1/2
p (不嫁|不帅、性格不好、身高矮、不上进) = ((1/61/211/2)1/2)/(1/31/37/12*1/3)
很显然(1/6*1/2*1*1/2) > (1/2*1/6*1/6*1/6*1/2)
于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进)
所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁!!!!
朴素贝叶斯分类的优缺点
优点:
(1) 算法逻辑简单,易于实现
(2)分类过程中时空开销小
缺点:
理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
常用朴素贝叶斯分类模型
依据特征值是连续还是离散选择
高斯朴素贝叶斯
Gaussian Naive Bayes是指当特征属性为连续值时,而且分布服从高斯分布,那么在计算P(x|y)的时候可以直接使用高斯分布的概率公式:假定: ,其中分别是第c类样本和第i个属性上取值的均值和方差。
伯努利朴素贝叶斯
Bernoulli Naive Bayes是指当特征属性为连续值时,而且分布服从伯努利分布,那么在计算P(x|y)的时候可以直接使用伯努利分布的概率公式:
伯努利分布是一种离散分布,只有两种可能的结果。1表示成功,出现的概率为p;0表示失败,出现的概率为q=1-p;其中均值为E(x)=p,方差为Var(X)=p(1-p)
多项式朴素贝叶斯(引入平滑项)
Multinomial Naive Bayes是指当特征属性服从多项分布(特征是离散的形式的时候),直接计算类别数目的占比作为先验概率和条件概率。
N是总样本个数,k是总的类别个数,Nyk是类别为yk的样本个数,α为平滑值。
是类别为的样本个数,为特征属性的不同取值数目,,为类别中第i维特征的值为的样本个数,α为平滑值。
当α=1时,称为Laplace平滑,当0<α<1时,称为Lidstone平滑,α=0时不做平滑;平滑的主要作用是可以克服条件概率为0的问题。(当存在0时,整个式子*0为0)
即,当某一特征属性为0时,我们通过分子+α来避免,为0,即人为增加一样本,此时为确保公平,任一特征属性下都应该加1样本。平滑项(参考https://zhuanlan.zhihu.com/p/26329951)
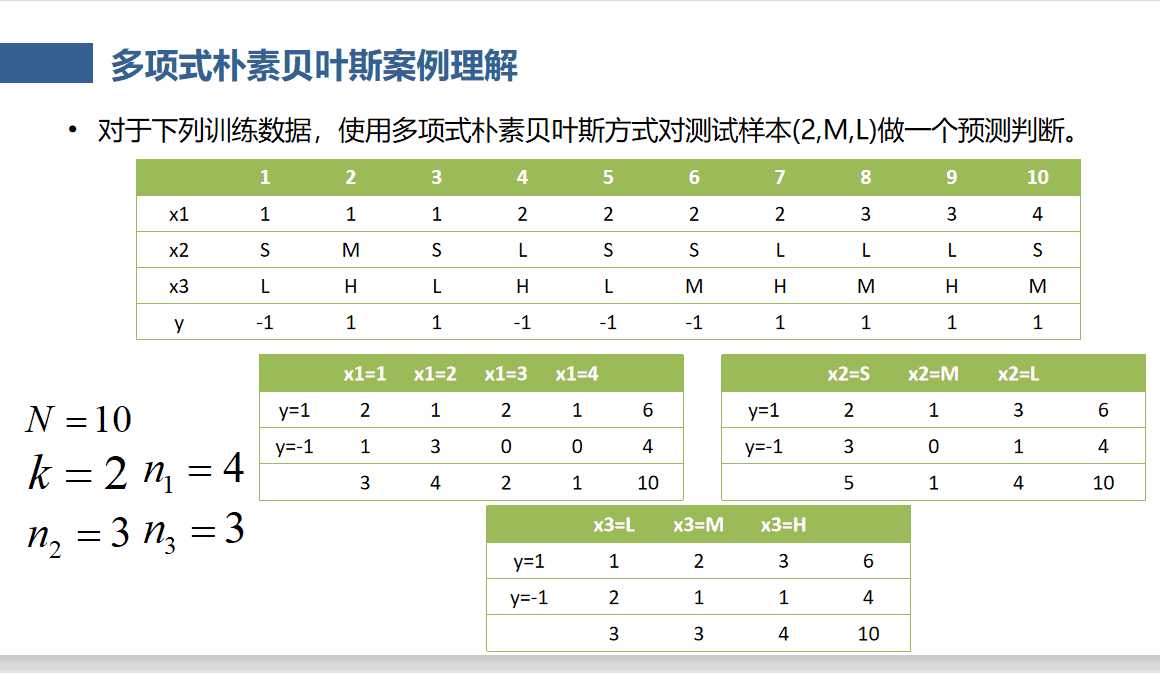
多项式朴素贝叶斯案例理解(平滑项作用举例)
(参考文章末尾附带PPT 13-16)
贝叶斯网络
- 把某个研究系统中涉及到的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。
- 贝叶斯网络(Bayesian Network),又称有向无环图模型(directed acyclic graphical model, DAG),是一种概率图模型,根据概率图的拓扑结构,考察一组随机变量{X1,X2,…,Xn}及其N组条件概率分布(Conditional Probabililty Distributions, CPD)的性质。
- 当多个特征属性之间存在着某种相关关系的时候,使用朴素贝叶斯算法就没法解决这类问题,那么贝叶斯网络就是解决这类应用场景的一个非常好的算法。
- 一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,可以是可观察到的变量,或隐变量,未知参数等等。连接两个节点之间的箭头代表两个随机变量之间的因果关系(也就是这两个随机变量之间非条件独立),如果两个节点间以一个单箭头连接在一起,表示其中一个节点是“因”,另外一个是“果”,从而两节点之间就会产生一个条件概率值。
- 贝叶斯网络的关键方法是图模型,构建一个图模型我们需要把具有因果联系的各个变量用箭头连在一起。贝叶斯网络的有向无环图中的节点表示随机变量。连接两个节点的箭头代表此两个随机变量是具有因果关系的。
- 贝叶斯网络是模拟人的认知思维推理模式的,用一组条件概率以及有向无环图对不确定性因果推理关系建模
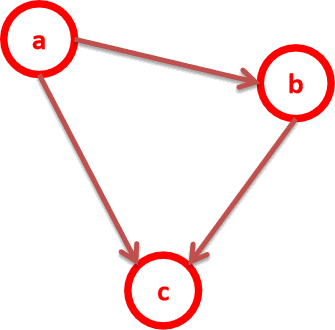
最简单的一个贝叶斯网络:P(a,b,c ) = P(c|a.b)P(b|a)P(a)
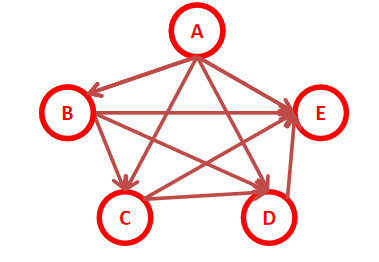
全连接贝叶斯网络:每一对节点都有边连接:
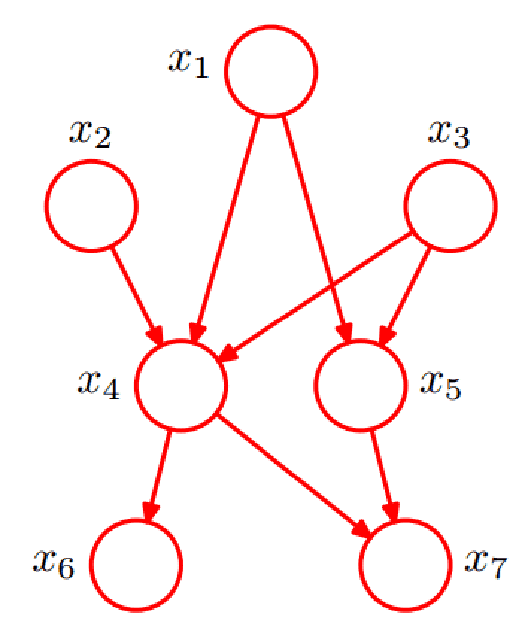
- x6和x7在给定条件下独立
- x1,x2,x3…x7的联合分布为
举例:详见文末PPT 29-30
贝叶斯网络判定条件独立(贝叶斯网络的结构形式)
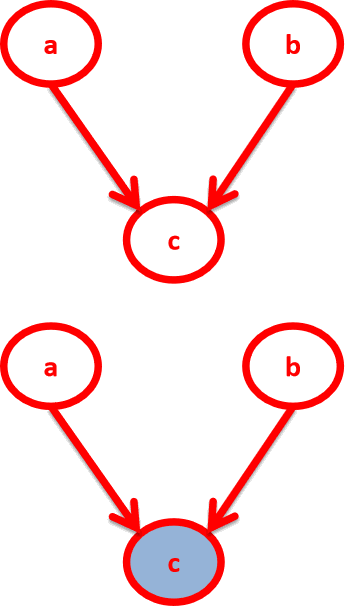
1.head - to - head
在C未知的情况下,a和b被阻断(blocked),是独立的
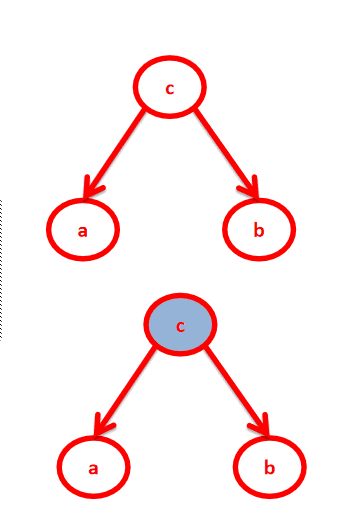
2.head- to -tail
在C给定的条件下,a和b被阻断(blocked)是独立的:
P(a,b,c)=P(a)P(c|a)P(b|c)
c未知时,有:P(a,b,c)=P(a)*P(c|a)*P(b|c),但无法推出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
在C给定的条件下,a和b被阻断(blocked)是独立的
在c未知的时候,有:P(a,b,c)=P©*P(a|c)*P(b|c),此时,没法得出P(a,b) = P(a)P(b),即c未知时,a、b不独立。