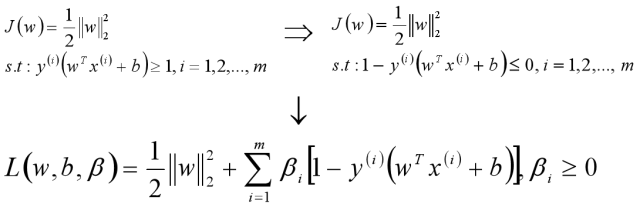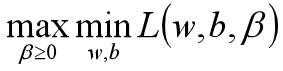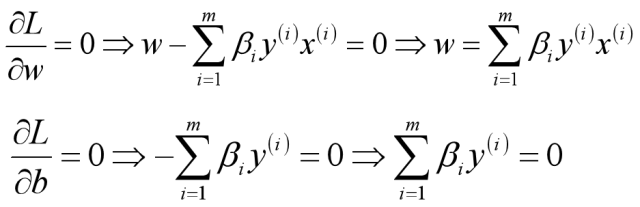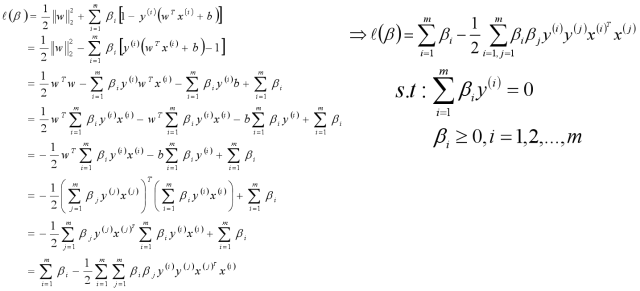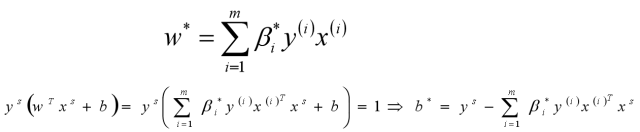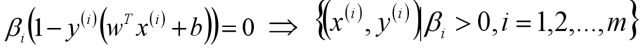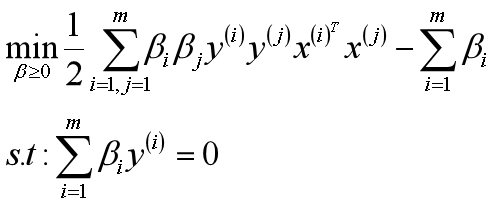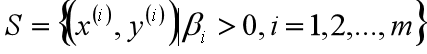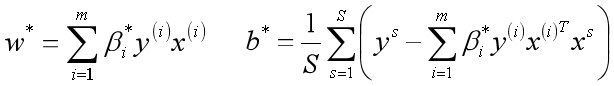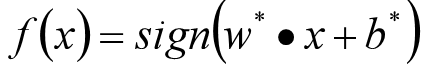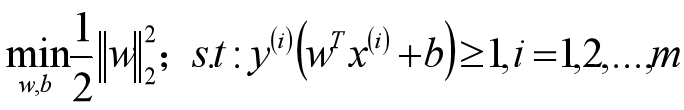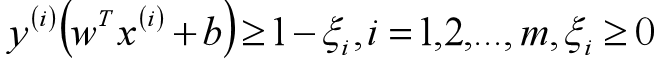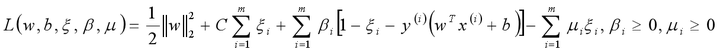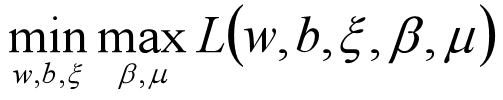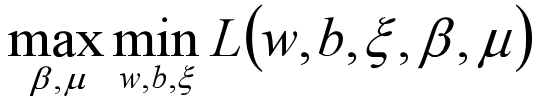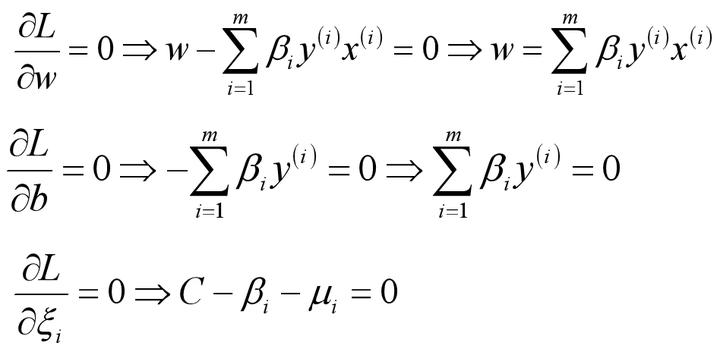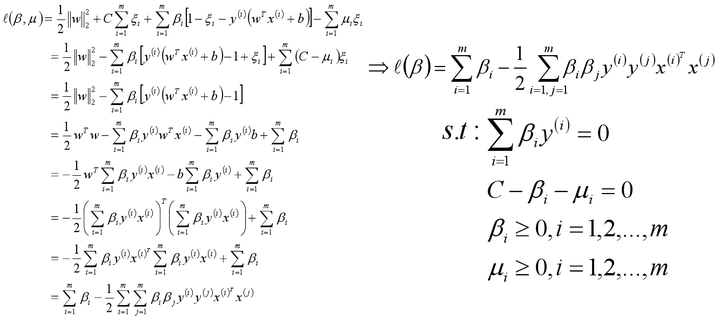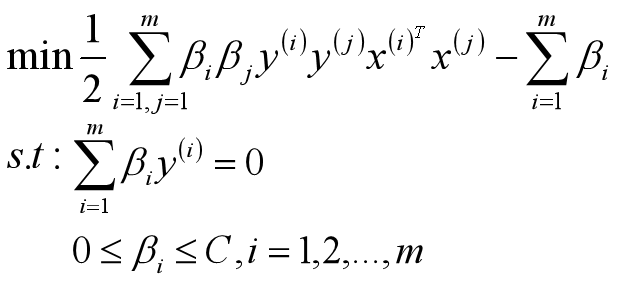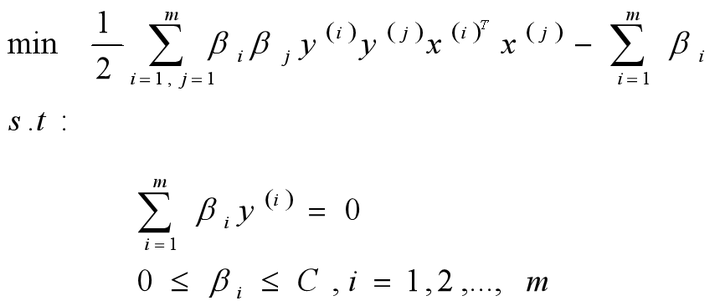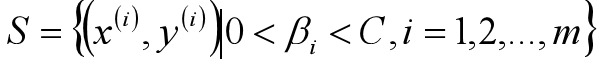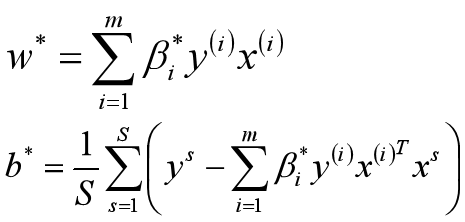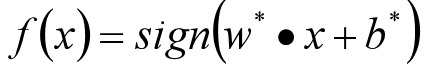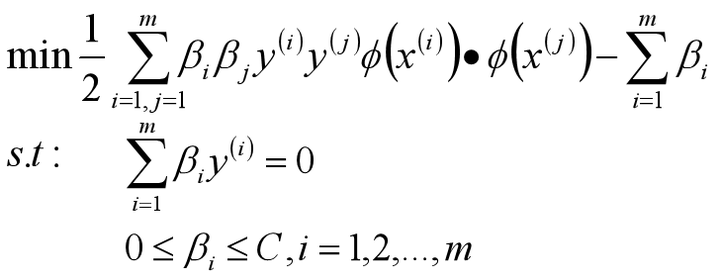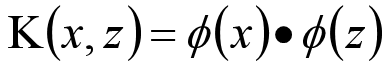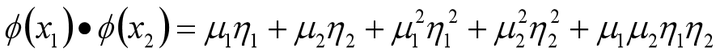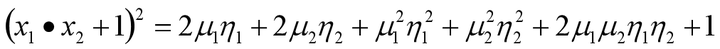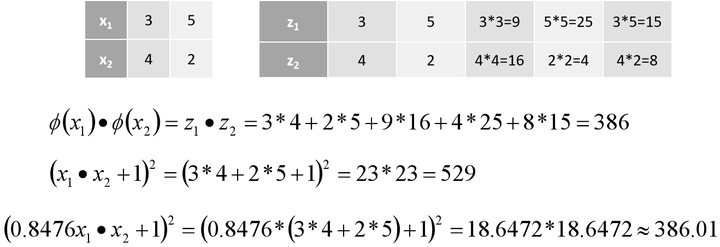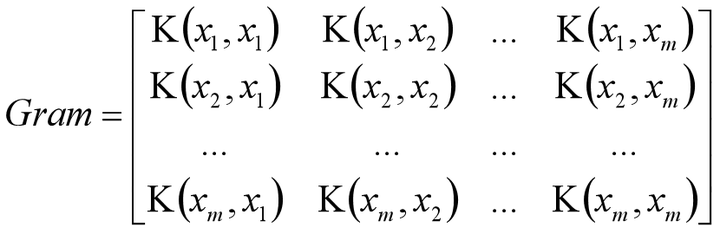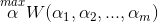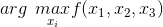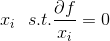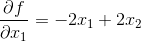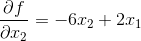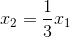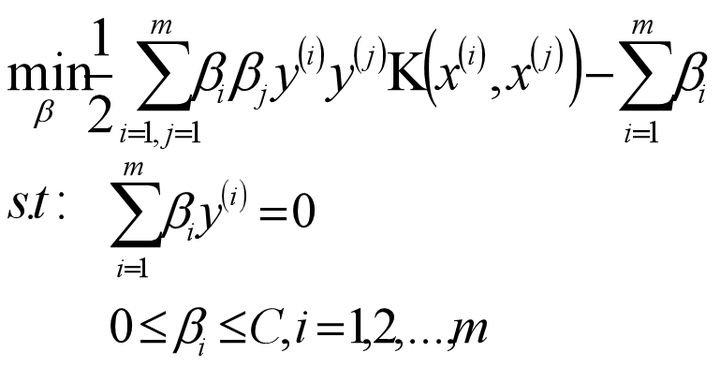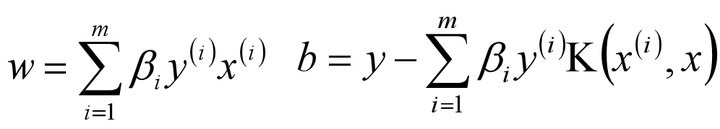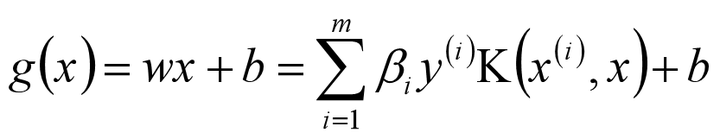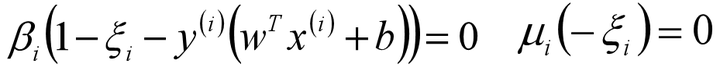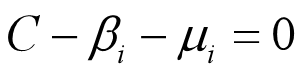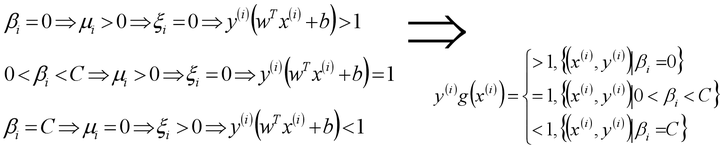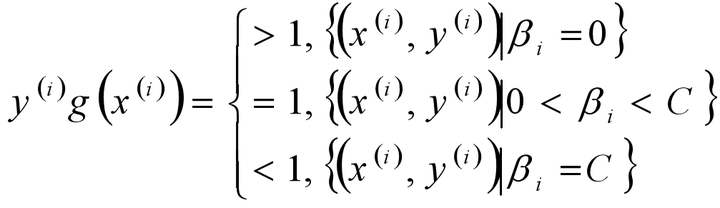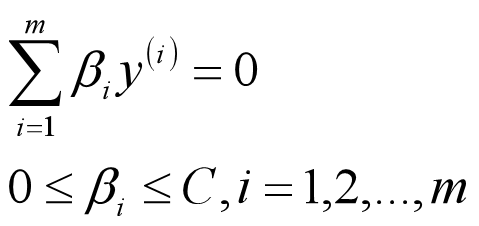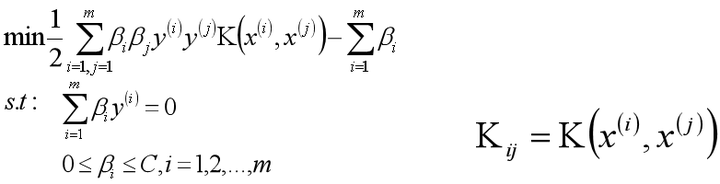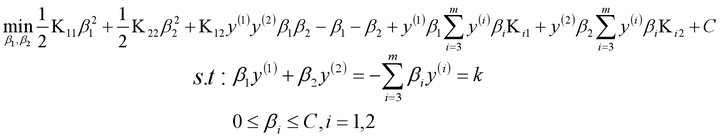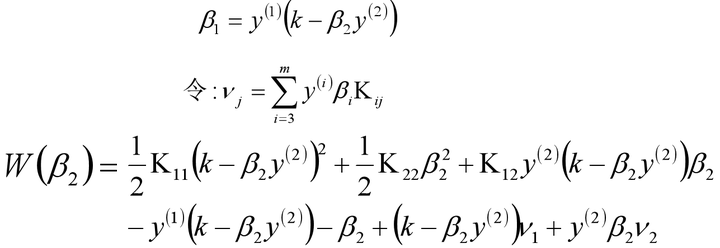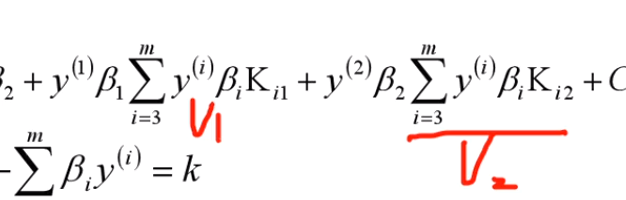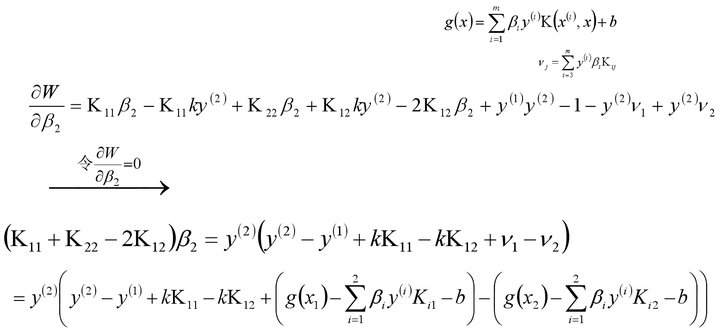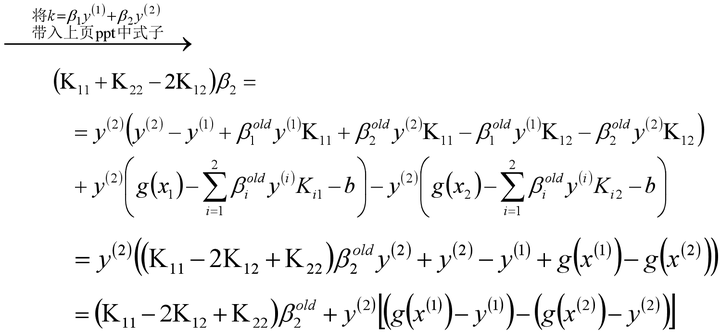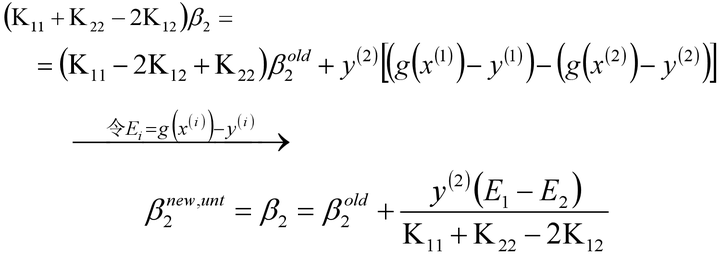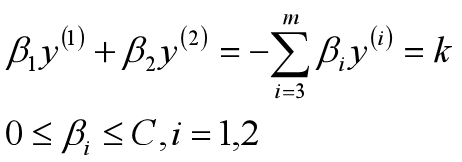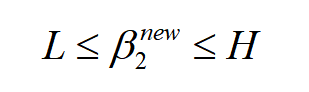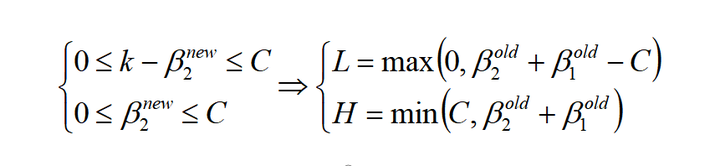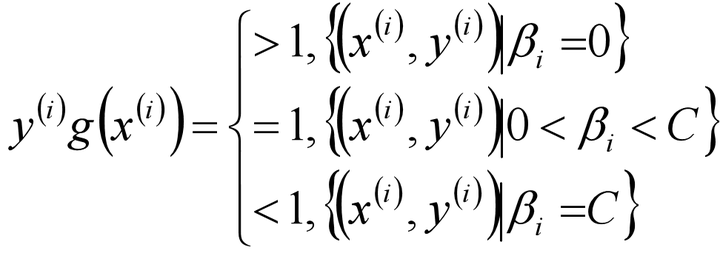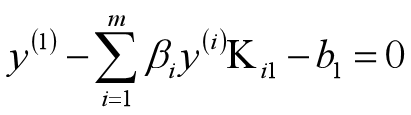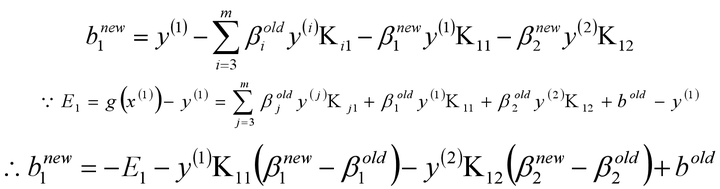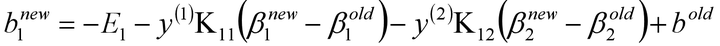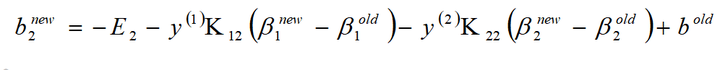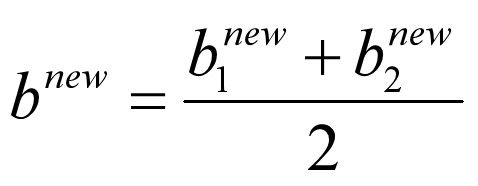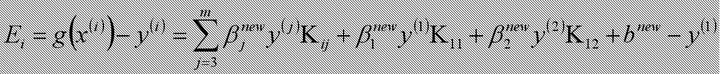感知机模型：

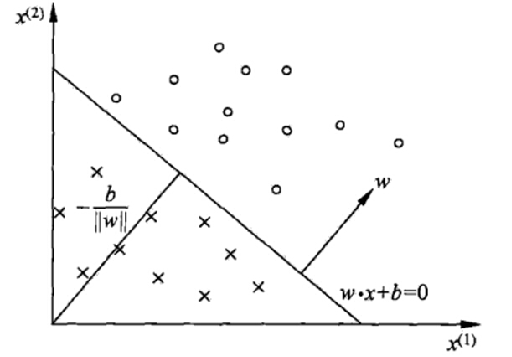
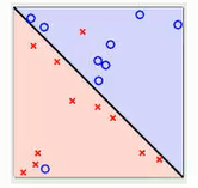
感知器模型是SVM、神经网络、深度学习等算法的基础;感知器模型就是试图找到一条直线，能够把所有的“+1”类和“-1”类分隔开，如果是高维空间中，感知器模型寻找的就是一个超平面，能够把所有的二元类别分割开。感知器模型的前提是：数据是线性可分的。

目标是找到一个超平面，即：

感知器模型为:

感知器模型正确分类（预测和实际类别一致）：yθx>0（y为实际值，θx为预测值），错误分类（预测和实际类别不一致）：yθx<0；所以我们可以定义我们的损失函数为：期望使分类错误的所有样本(k条样本)到超平面的距离之和最小。

即： (去绝对值符号，分类错误<0,分子加”—“)

简化损失函数：因为此时分子和分母中都包含了θ值，当分子扩大N倍的时候，分母也会随之扩大，也就是说分子和分母之间存在倍数关系，所以可以固定分子或者分母为1，然后求另一个即分子或者分母的倒数的最小化作为损失函数，简化后的损失函数为（分母为1）:

简化损失函数：因为此时分子和分母中都包含了θ值，当分子扩大N倍的时候，分母也会随之扩大，也就是说分子和分母之间存在倍数关系，所以可以固定分子或者分母为1，然后求另一个即分子或者分母的倒数的最小化作为损失函数，简化后的损失函数为（分母为1）: (即 ,分子分母相抵消，模长对结果无影响)。

直接使用梯度下降法就可以对损失函数求解，不过由于这里的k是分类错误的样本点集合，不是固定的，所以我们不能使用批量梯度下降法(BGD)求解，只能使用随机梯度下降(SGD)或者小批量梯度下降(MBGD)；一般在感知器模型中使用SGD来求解。

SVM(支持向量机)

支持向量机(Support Vecor Machine, SVM)本身是一个二元分类算法，是对感知器算法模型的一种扩展，现在的SVM算法支持线性分类和非线性分类的分类应用，并且也能够直接将SVM应用于回归应用中，同时通过OvR或者OvO的方式我们也可以将SVM应用在多元分类领域中。在不考虑集成学习算法，不考虑特定的数据集的时候，在分类算法中SVM可以说是特别优秀的。

在感知器模型中，算法是在数据中找出一个划分超平面，让尽可能多的数据分布在这个平面的两侧，从而达到分类的效果，但是在实际数据中这个符合我们要求的超平面是可能存在多个的。

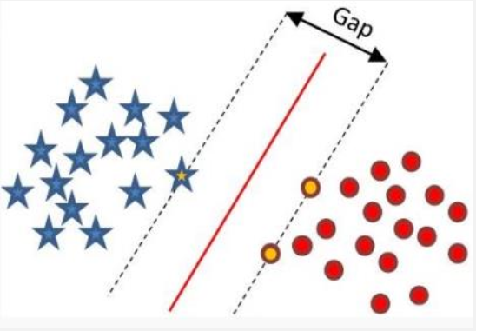
SVM思想：在感知器模型中，我们可以找到多个可以分类的超平面将数据分开，并且优化时希望所有的点(预测正确的点)都离超平面尽可能的远，但是实际上离超平面足够远的点基本上都是被正确分类的，所以这个是没有意义的；反而比较关心那些离超平面很近的点，这些点比较容易分错。所以说我们只要让离超平面比较近的点尽可能的远离这个超平面，那么我们的模型分类效果应该就会比较不错。SVM其实就是这个思想。

名词概念：

线性可分(Linearly Separable)：在数据集中，如果可以找出一个超平面，将两组数据分开，那么这个数据集叫做线性可分数据。
线性不可分(Linear Inseparable)：在数据集中，没法找出一个超平面，能够将两组数据分开，那么这个数据集就叫做线性不可分数据。
分割超平面(Separating Hyperplane)：将数据集分割开来的直线/平面叫做分割超平面。
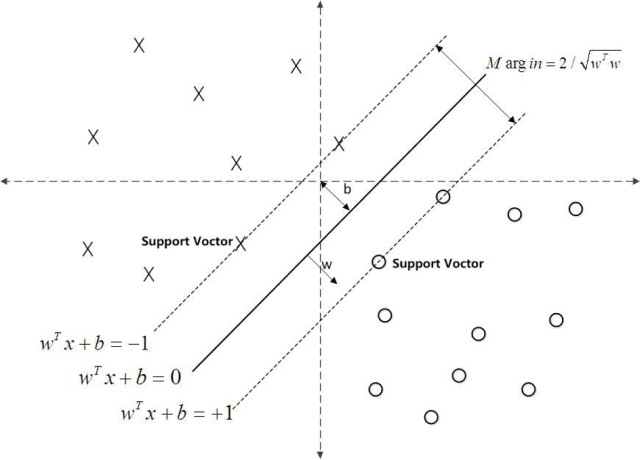
支持向量(Support Vector)：离分割超平面最近的那些点叫做支持向量。
间隔(Margin)：支持向量数据点到分割超平面的距离称为间隔。

支持向量到超平面的距离为：在SVM中支持向量到超平面的函数距离一般设置为1

∵

∴

SVM模型是让所有的分类点在各自类别的支持向量远离超平面的一侧，同时要求支持向量尽可能的远离这个超平面，用数学公式表示如下：

W^{T}=(w_1,w_2,…,w_n)

(s.t: 指”受限制于…“)

(对偶问题）

则SVM原始目标函数/损失函数为：

将此时的目标函数和约束条件使用KKT条件转换为拉格朗日函数，从而转换为无约束的优化函数。

引入拉格朗日乘子后，优化目标变成：

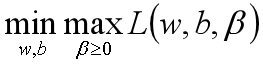g(x)小于等于0 当L取最大值 g(x)等于0 消去g(x) KKT条件分析

根据拉格朗日对偶化特性，将该优化目标转换为等价的对偶问题来求解，从而优化目标变成：

所以对于该优化函数而言，可以先求优化函数对于w和b的极小值，然后再求解对于拉格朗日乘子β的极大值。

首先求让函数L极小化的时候w和b的取值，这个极值可以直接通过对函数L分别求w和b的偏导数得到：

将求解出来的w和b带入优化函数L中，定义优化之后的函数如下：

通过对w、b极小化后，我们最终得到的优化函数只和β有关，所以此时我们可以直接极大化我们的优化函数，得到β的值，从而可以最终得到w和b的值。β值的求解使用SMO算法

假设存在最优解β*；根据w、b和β的关系，可以分别计算出对应的w值和b值(一般使用所有支持向量的计算均值来作为实际的b值)；

这里的(xs,ys)即支持向量，根据KKT条件中的对偶互补条件(松弛条件约束)，支持向量必须满足一下公式：

2.线性可分SVM算法流程：

输入线性可分的m个样本数据{(x1,y1),(x2,y2),…,(xm,ym)}，其中x为n维的特征向量，y为二元输出，取值为+1或者-1；SVM模型输出为参数w、b以及分类决策函数。
构造约束优化问题；

使用SMO算法求出上式优化中对应的最优解β*；

找出所有的支持向量集合S;

更新参数w*、b*的值；

构建最终的分类器；

线性可分SVM总结

\1. 要求数据必须是线性可分的；

\2. 纯线性可分的SVM模型对于异常数据的预测可能会不太准；

\3. 对于线性可分的数据，线性SVM分类器的效果非常不错。

SVM的软间隔模型

线性可分SVM中要求数据必须是线性可分的，才可以找到分类的超平面，但是有的时候线性数据集中存在少量的异常点，由于这些异常点导致了数据集不能够线性划分；直白来讲就是：正常数据本身是线性可分的，但是由于存在异常点数据，导致数据集不能够线性可分；

如果线性数据中存在异常点导致没法直接使用SVM线性分割模型的时候，我们可以通过引入软间隔的概念来解决这个问题；

硬间隔：可以认为线性划分SVM中的距离度量就是硬间隔，在线性划分SVM中，要求函数距离一定是大于1的，最大化硬间隔条件为：

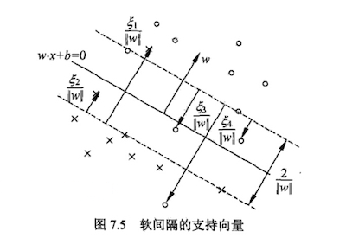
软间隔：SVM对于训练集中的每个样本都引入一个松弛因子(ξ)，使得函数距离加上松弛因子后的值是大于等于1；这表示相对于硬间隔，对样本到超平面距离的要求放松了。(引入松弛因子(ξ))

松弛因子(ξ)越大，表示样本点离超平面越近，如果松弛因子大于1，那么表示允许该样本点分错，所以说加入松弛因子是有成本的，过大的松弛因子可能会导致模型分类错误，所以最终的目标函数就转换成为：

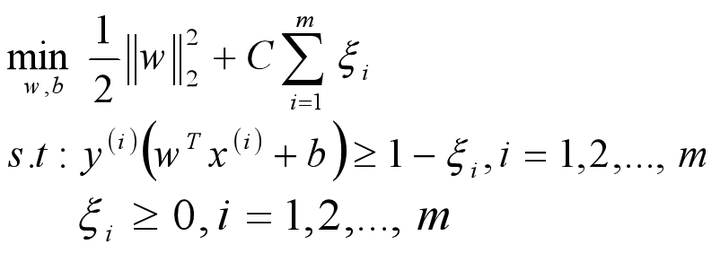注：函数中的C&amp;amp;amp;amp;amp;amp;amp;gt;0是惩罚参数，是一个超参数，类似L1/L2 norm的参数；C越大表示对误分类的惩罚越大，也就是越不允许存在分错的样本；C越小表示对误分类的惩罚越小，也就是表示允许更多的分错样本存在；C值的给定需要调参。

同线性可分SVM，根据KKT条件构造软间隔最大化的约束问题对应的拉格朗日函数如下：

从而将我们的优化目标函数转换为：

优化目标同样满足KKT条件，所以使用拉格朗日对偶将优化问题转换为等价的对偶问题：

先求优化函数对于w、b、ξ的极小值，这个可以通过分别对优化函数L求w、b、ξ的偏导数得，从而可以得到w、b、ξ关于β和μ之间的关系。

将w、b、ξ的值带入L函数中，就可以消去优化函数中的w、b、ξ，定义优化之后的函数如下：

最终优化后的目标函数/损失函数和线性可分SVM模型基本一样，除了约束条件不同而已，也就是说也可以使用SMO算法来求解。

在硬间隔最大化的时候，支持向量比较简单，就是离超平面的函数距离为1的样本点就是支持向量。
在软间隔中，根据KKT条件中的对偶互补条件: β(1-ξ-y(wx+b))=0和μ(-ξ)=0，以及C-β-μ=0；从而有：
当0<βi≤C的时候，并且ξi=0的样本点均是支持向量(即所有的0<βi
当0<βi
注：软间隔和硬间隔中的支持向量的规则是一样的；
则x1是支持变量

SVM的软间隔模型算法流程：

输入线性可分的m个样本数据{(x1,y1),(x2,y2),…,(xm,ym)}，其中x为n维的特征向量，y为二元输出，取值为+1或者-1；SVM模型输出为参数w、b以及分类决策函数。

step 1:选择一个惩罚系数C>0，构造约束优化问题；

Step2:使用SMO算法求出上式优化中对应的最优解β*；
step3:找出所有的支持向量集合S;

step4:更新参数w*、b*的值；

step5:构建最终的分类器

SVM的软间隔模型总结

\1. 可以解决线性数据中携带异常点的分类模型构建的问题；
\2. 通过引入惩罚项系数(松弛因子)，可以增加模型的泛化能力，即鲁棒性；
\3. 如果给定的惩罚项系数C越小，表示在模型构建的时候，就允许存在越多的分类错误的样本，也就表示此时模型的准确率会比较低；如果惩罚项系数越大，表示在模型构建的时候，就越不允许存在分类错误的样本，也就表示此时模型的准确率会比较高。

非线性可分SVM

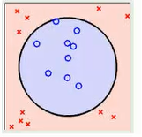
不管是线性可分SVM还是加入惩罚系数后的软间隔线性可分SVM其实都要求数据本身是线性可分的，对于完全不可以线性可分的数据，这两种算法模型就没法解决这个问题了

结合多项式回归在处理非线性可分数据时候的作用，在SVM的线性不可分的数据上，如果将数据映射到高维空间中，那么数据就会变成线性可分的，从而就可以使用线性可分SVM模型或者软间隔线性可分SVM模型。也就是说，对于线性不可分SVM模型来讲，重点在于低维特征数据到高维特征数据之间的映射。

定义一个从低维特征空间到高维特征空间的映射函数Ф，非线性可分SVM的优化目标函数：

可以看到的是，只需要将原来的低维空间中的两个向量的点积转换为高维空间中两个向量的点积即可。

问题：这样一来问题就解决了吗？似乎是的：拿到非线性数据，就找一个映射，然后一股脑把原来的数据映射到新空间中，再做线性 SVM 即可。不过事实上没有这么简单！其实刚才的方法稍想一下就会发现有问题：在最初的例子里做了一个二阶多项式的转换，对一个二维空间做映射，选择的新空间是原始空间的所有一阶和二阶的组合，得到了5个维度；如果原始空间是三维，那么我们会得到9维的新空间；如果原始空间是n维，那么我们会得到一个n(n+3)/2维的新空间**；这个数目是呈爆炸性增长的，这给计算带来了非常大的困难，而且如果遇到无穷维的情况，就根本无从计算。**

2.核函数

假设函数Ф是一个从低维特征空间到高维特征空间的一个映射，那么如果存在函数K(x,z), 对于任意的低维特征向量x和z，都有：

称函数K(x,z)为核函数(kernal function)：在低维空间上的计算值等价于向量做维度扩展后的点乘的结果。核函数在解决线性不可分问题的时候，采取的方式是：使用低维特征空间上的计算来避免在高维特征空间中向量内积的恐怖计算量；也就是说此时SVM模型可以应用在高维特征空间中数据可线性分割的优点，同时又避免了引入这个高维特征空间恐怖的内积计算量。

即：用低维空间中少的内积的计算量来让模型具有高维空间中的线性可分的优点。

例：，设两个向量和，而即是到前面说的五维空间的映射，因此映射过后的内积为：

而同时我们可以发现有一下公式

可以发现两者之间非常相似，所以我们只要乘上一个相关的系数，就可以让这两个式子的值相等，这样不就将五维空间的一个内积转换为两维空间的内积的运算。

现有有两个两维的向量，进行二阶多项式扩展，然后进行内积计算，这个时候映射高维后计算的计算量为：11次乘法+4次加法；采用近似计算的计算量为：3次乘法+2次加法；采用加系数后的近似计算的计算量为：4次乘法+2次加法；

核函数总结

\1. 核函数可以自定义；核函数必须是正定核函数，即Gram矩阵是半正定矩阵；

\2. 核函数的价值在于它的效果相当于将特征进行从低维到高维的转换，但核函数它是在低维空间上的计算，而将实质上的分类效果表现在了高维上，也就如上文所说的避免了直接在高维空间中的复杂计算；

\3. 通过核函数，可以将非线性可分的数据转换为线性可分数据；

SVR

做回归用，了解即可

坐标下降（上升）法原理(搬运自https://blog.csdn.net/u010626937/article/details/75044343)

假设要求解下面的优化问题：

在这里，我们需要求解m个变量αi，一般来说是通过梯度下降（这里是求最大值，所以应该叫上升）等算法来求解，每一次迭代对所有m个变量αi也就是α向量进行一次性优化。（这里指的是一个向量的所有分量）。通过每次迭代中的误差调整α向量中每个元素的值。而坐标上升法（坐标上升与坐标下降可以看做是一对，坐标上升是用来求解max最优化问题，坐标下降用于求min最优化问题）的思想是每次迭代只调整一个变量αi的值，其他变量的值在这次迭代中固定不变。(这里指的是一个向量中的一个分量)。

最里面语句的意思是固定除αi之外的所有αj(i不等于j)，这时W可看作只是关于αi的函数，那么直接对αi求导优化即可。这里我们进行最大化求导的顺序i是从1到m，可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优，那么坐标上升法会是一个很高效的求极值方法。

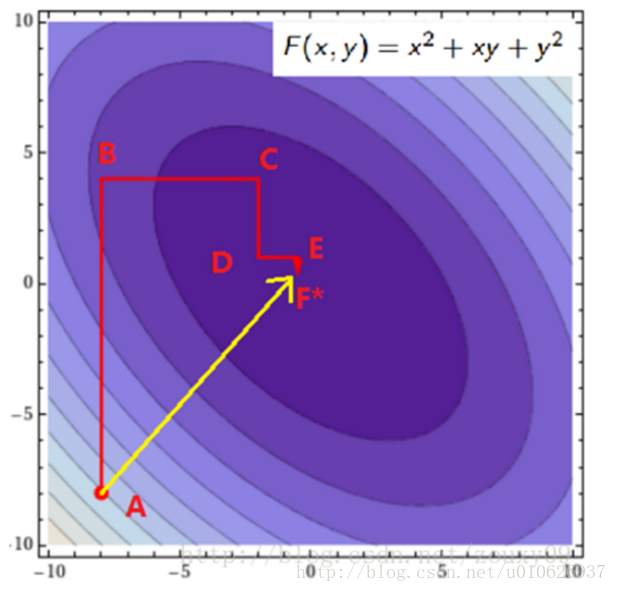
用个二维的例子来说明下坐标下降法：我们需要寻找f(x,y)=x2+xy+y2的最小值处的(x*, y*)，也就是下图的F*点的地方.

假设我们初始的点是A（图是函数投影到xoy平面的等高线图，颜色越深值越小），我们需要达到F的地方。那最快的方法就是图中黄色线的路径，一次性就到达了，其实这个是牛顿优化法，但如果是高维的话，这个方法就不太高效了（因为需要求解矩阵的逆，这个不在这里讨论）。我们也可以按照红色所指示的路径来走。从A开始，先固定x，沿着y轴往让f(x, y)值减小的方向走到B点，然后固定y，沿着x轴往让f(x, y)值减小的方向走到C点，不断循环，直到到达F。反正每次只要我们都往让f(x, y)值小的地方走就行了，这样脚踏实地，一步步走，每一步都使f(x, y)慢慢变小，总有一天，皇天不负有心人的。到达F*也是时间问题。到这里你可能会说，这红色线比黄色线贫富差距也太严重了吧。因为这里是二维的简单的情况嘛。如果是高维的情况，而且目标函数很复杂的话，再加上样本集很多，那么在梯度下降中，目标函数对所有αi求梯度或者在牛顿法中对矩阵求逆，都是很耗时的。这时候，如果W只对单个αi优化很快的时候，坐标下降法可能会更加高效。

数学例题讲解

下面以如下的优化问题为例：

在迭代的过程中，每次固定x2更新x1，在确定了x1的条件下，固定x1，更新x2。即每次迭代求解：

也即求解

，假设我们首先固定x2,来更新x1：

令其为0，得到：

再固定x1，得到：

令其为0，得到：

不断按照上述的过程，直到算法收敛。

七、SMO（可略过）

序列最小优化算法(Sequential minimal optimization, SMO)是一种用于解决SVM训练过程中所产生的优化问题的算法。于1998年由John Platt发明。SMO的思想类似坐标上升算法，我们需要优化一系列的αα的值，我们每次选择尽量少的来优化，不断迭代直到函数收敛到最优值。